Harmonic Analysis of Current Velocity
From BAWiki
Motivation
For almost any location within an estuary the current velocity can be decomposed into a periodic part driven by the tides (astronomical and shallow water tides) as well as a non-periodic part driven by river runoff, meteorological effects as well as local topographic features.
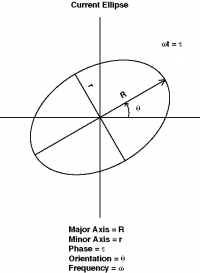
For each tidal constituent the tip of the current velocity vector describes an ellipse, the tidal ellipse (see accompanying figure). Within each period of the respective tidal constituent a full rotation is executed. Characteristic parameters for a tidal ellipse are semi major axis, semi minor axis, inclination of tidal ellipse as well as its eccentricity. In dependence on eccentricity the ellipse degenerates either to a circle (eccentricity +1.0 or -1.0) or a straight line (eccentricity 0.0). The beforementioned parameters are well suited to describe the tidal influence on current velocity.
Basic Concepts
Basic informations on Tidal Harmonic Analysis are presented in Harmonic Analysis of Water Level. The methods used to compute various ellipse parameters using program NCANALYSE are described in more detail in publication zhigang_xu_2000_ellipse_parameters_conversion.pdf.
The computational procedure is as follows (number of equation with reference to Zhigang Xu (2000) given in brackets):
- Compute amplitude and phase for u-component (x- or eastward) of current velocity (Eq. 1).
- Compute amplitude and phase for v-component (y- or northward) of current velocity (Eq 2).
- Determine equivalent complex formulas for u and v (Eq. 9 und Eq. 10).
- Derive complex formulas for (mathematical) positive as well as negative rotating circular components (Eq. 7 and Eq. 8). Superposition of two components with different sense of orientation results in a tidal ellipse.
- From the lastly mentioned complex formulas magnitude an phase for positive and negative rotating components can be computed.
- With these results it is possible to compute semi major axis and semi minor axis (Eq. 14 and Eq. 19), axes inclination (Eq. 15 and Eq. 20) as well as eccentricity (Eq. 21).
The aforementioned calculations must be performed for any tidal constituent.
Definition of Characteristic Numbers
The Least Square Fit Method (LSQF) is used to compute amplitude and phase for the u- and v-component of current velocity. For this purpose program NCANALYSE makes use of methods available within the software package LAPACK.
All quantities are computed for permanently wet areas only.
For each tidal constituent the following quantities are determined.
Residual Current Velocity (Vres)
Residual current velocity (computed from tidal constituent analysis) within the period of data analysis. This quantity describes the non-tidal (or non-periodc) contribution. It mainly depends on river flow, meteorology and local topographic details, but is also dependent to some extent on the number of tidal constituents taken into account.
Amplitude and Phase of Tidal Constituents
The subsequent quantities are essential to derive the various characteristic parameters for tidal ellipses introduced below. Standard error for each of the four quantities is also computed. The quantities, although important, are not well suited to be used for visualization.
Amplitude of u-Component
Amplitude of current velocity u-component (x- or eastward) of a tidal constituent.
Amplitude of v-Component
Amplitude of current velocity v-component (y- or northward) of a tidal constituent.
Phase of u-Component
Phase (in degree) of current velocity u-component (x- or eastward) of a tidal constituent.
Phase of v-Component
Phase (in degree) of current velocity v-component (y- or northward) of a tidal constituent.
Characteristic Parameters for Tidal Ellipses
From the above mentioned quantities (amplitudes and phases) all subsequent characteristic parameters for tidal ellipses can be derived.
Semi Major Axis of Tidal Ellipse
Semi major axis of a tidal constituent. Gives maximum current velocity within one period for the tidal constituent.
Semi Minor Axis of Tidal Ellipse
Semi minor axis of a tidal constituent. Gives minimum current velocity within one period for the tidal constituent.
Inclination (direction) of Major Axis
Gives the (mathematically positive) direction (-180.0 to 180.0 degree) of the semi major axis for a tidal constituent velocity. Is equivalent to the orientation of the maximum current induced by the tidal constituent.
Inclination (direction) of Minor Axis
Gives the (mathematically positive) direction (-180.0 to 180.0 degree) of the semi minor axis for a tidal constituent velocity. Is equivalent to the orientation of the minimum current induced by the tidal constituent.
Eccentricity of Tidal Ellipse
Eccentricity is defined as the ratio between semi minor and semi major axis of a tidal ellipse. Special cases are:
- 0.0 : rectilinear current, e. g. due to topographic guidance;
- 1.0 : circular current velocity in mathematical positive direction (counter clockwise);
- -1.0 : circular current velocity in mathematical negative direction (clockwise).
Phase of maximum Current Velocity
Phase (in dgree) of maximum current velocity for a tidal constituent. Restricted range -180 to 180 degree.
Phase of minimum Current Velocity
Phase (in dgree) of minimum current velocity for a tidal constituent. Restricted range -180 to 180 degree.
Flow Duration Asymmetry (Skewness FDA)
This parameter describes differences in the flow velocities around flood slack compared to those around ebb slack. Positive values indicate smaller velocities around flood slack. Please notice that a residual current is neglected in the formulas used.
Skewness FDA
Computation of skewness FDA (sum over all contributions of tidal constituents) according to Song (2011), Eq. 16 from amplitude, phase and frequency of tidal constituents.
Skewness FDA for all pairs and triplets
Computation of skewness FDA for all pairs and triplets of suitable tidal constituents according to Song (2011), Eq. 20 and Eq. 21 from amplitude, phase and frequency of contributing tidal constituents.
Flow Velocity Asymmetry (Skewness FVA)
This parameter describes differences between maximum flood current and ebb current velocities. Positive values indicate larger flood current velocities. Please notice that a residual current is taken into account in the formulas used.
Skewness FVA
Computation of skewness FVA (sum over all contributions of tidal constituents and a residual current) according to Gong (2016), Eq. 24 from amplitude and phase of the tidal constituents as well as a residual current.
Skewness FVA for all pairs and triplets
Computation of skewness FVA for all pairs and triplets formed out of suitable tidal constituents according to Gong (2016), Eq. 24 from amplitude and phase of the tidal constituents as well as a residual current.
Skewness FVA from residual current
Computation of skewness resulting from a residual current according to Gong (2016), Eq. 24 from amplitude and phase of the tidal constituents as well as a residual current.
back to Analysis of Calculated Results
