Mathematisches Verfahren UNTRIM2
Aus BAWiki
Kurzbeschreibung
Das mathematische Verfahren UNTRIM2 ist eng mit den Verfahren UNTRIM und UNTRIM2007 verwandt. UNTRIM2 ist ein semi-implizites Finite-Differenzen (-Volumen) Verfahren zur numerischen Lösung der dreidimensionalen Flachwassergleichungen sowie der dreidimensionalen Transportgleichung für Salz, Wärme, Schwebstoffe sowie suspendierte Sedimente. Als wesentliche Neuerung gegenüber den klassischen UNTRIM-Verfahren kann die Bathymetrie des Modellgebietes mit Hilfe der SubGrid-Technologie wesentlich genauer als bisher, und unabhängig von der Auflösung des Berechnungsgitters, wiedergegeben werden.
SubGrid-Technologie
Berechnungsgitter und SubGrid
- Berechnungsgitter:
- Es wird ein unstrukturiertes orthogonales Gitter (UOG) benutzt. Hierbei wird das Lösungsgebiet von einer endlichen Anzahl konvexer Polygone überlappungsfrei überdeckt. Ein Gitter entspricht genau dann einem UOG, wenn innerhalb eines jeden Polygons ein Punkt (Zentrum) bestimmt werden kann, so dass jede Verbindungslinie zu einem Zentrum eines Nachbarpolygons die gemeinsame Seite der Polygone senkrecht schneidet.
- SubGrid:
- Die Modelltopografie wird auf dem SubGrid wiedergegeben. Die Auflösung des SubGrid kann deutlich größer als die des Berechnungsgitters sein.
- Nichtlinearitäten:
- Das Wasservolumen in einem Berechnungspolygon ist nichtlinear vom Wasserstand abhängig.
- Die durchströmte Fläche entlang einer Kante kann ebenfalls nichtlinear vom Wasserstand abhängen.
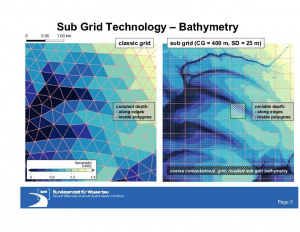
In dem Bild Wattgebiet der Elbe wird die diskrete Topografie sowohl im klassischen Gitter (links) als auch im Gitter mit SubGrid (rechts) dargestellt. In dem klassischen, aus Dreiecken aufgebauten, unstrukturierten Gitter, variiert die Tiefe in einem Polygon sowie entlang einer Kante nicht. Wird demgegenüber in einem Berechnungsgitter die SubGrid-Technologie zur Diskretisierung der Bathymetrie genutzt, so erkennt man sehr schnell den großen Detailreichtum dieses Wattgebiets. Dies ist darauf zurückzuführen, dass bei Verwenden der SubGrid-Technologie die Tiefe in jedem Polygon und entlang einer jeden Kante veränderlich sein kann, und somit auch kleinräumige topografische Strukturen naturgetreu in dem Modell wiedergegeben werden können.
Berechnungsergebnisse
Die Ergebnisse für z. B. Wasserstand und Strömung liegen auf dem (groben) Berechnungsgitter und nicht auf dem (feineren) SubGrid vor. Typischer Weise entspricht der Wasserstand dem mittleren Wasserstand innerhalb eines Polygons, und die Strömungsgeschwindigkeit gibt für jede Kante jeweils den Mittelwert für die aktuell durchströmte Fläche wieder.
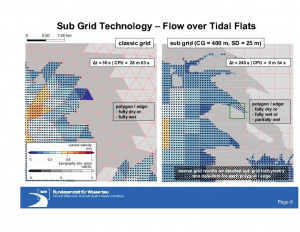
In dem Bild Synoptische Strömung im Wattgebiet der Elbe wird links die Strömung für das klassische, und rechts für das Gitter mit SubGrid dargestellt. Man erkennt, dass im klassischen Fall jedes Polygon nur gänzlich von Wasser bedeckt oder vollkommen trockengefallen sein kann. In dem Gitter mit SubGrid kann ein Polygon (und eine Kante) hingegen auch teilweise von Wasser bedeckt sein. Damit gelingt eine naturähnlichere Simulation der Überflutung von Wattgebieten, insbesondere das rasche Vordringen des Wassers entlang der tiefen Rinnen.
Vorteile
- Die Topografie kann unabhängig von der Auflösung des Berechnungsgitters beschrieben werden.
- Die Genauigkeit, mit der die Topografie wiedergegeben werden kann, wird prinzipiell nur durch die Genauigkeit der gemessenen Daten begrenzt.
- Für jede Wasserspiegellage entspricht das Wasservolumen in dem Modell dem in der Natur vorhandenen Wasservolumen. Gleiches gilt für die durchströmten Querschnitte.
- Überflutete und trocken gefallene Gebiete können präzise beschrieben werden.
- Die gleiche Genauigkeit hinsichtlich der Diskretisierung der Bathymetrie wird mit SubGrid zu deutlich geringeren CPU-Kosten erzielt, als dies mit einem klassischen Berechnungsgitter, ohne SubGrid-Technologie, möglich wäre.
Physikalische Prozesse
- reynoldsgemittelte Navier-Stokes-Gleichung (RANS)
- lokale Beschleunigung (Massenträgheit)
- advektive Beschleunigung
- Coriolisbeschleunigung
- barotroper Druckgradient
- barokliner Druckgradient
- hydrostatische oder nicht-hydrostatische Druckverteilung
- horizontale turbulente Viskosität (lokal isotrop, zeit- und ortsvariabel)
- turbulente Viskosität in Vertikalrichtung unter Berücksichtigung der vertikalen Dichteschichtung
- Bodenreibung
- Impulseintrag durch den Wind
- Quellen und Senken
- horizontale seegangsinduzierte Beschleunigung (durch Radiation Stress)
- Transport konservativer Tracer
- lokale Veränderung
- advektiver Transport durch die Strömung
- optionaler flux limiter : Minmod, van Leer oder Superbee
- horizontale turbulente Diffusivität (lokal isotrop, zeit- und ortsvariabel)
- turbulente Diffusivität in Vertikalrichtung unter Berücksichtigung der vertikalen Dichteschichtung
- Sinkgeschwindigkeit, Deposition und Erosion (bei Schwebstoffen)
- Wärmeaustausch mit der Atmosphäre und der Gewässersohle (bei Wärmetransport)
- Quellen und Senken
- Senken mit unmittelbarer Wiedereinleitung an einem anderen Ort, mit der Möglichkeit zur Abwandlung z.B. der Einleitungstemperatur sowie des Einleitungssalzgehalts gegenüber den entsprechenden Entnahmewerten.
Berechnungsergebnisse
- Wasserspiegelauslenkung der freien Oberfläche
- Strömungsgeschwindigkeit
- Tracerkonzentration (z.B. Salzgehalt, Temperatur, Schwebstoffgehalt)
- hydrodynamischer Druck
Anmerkung: Bei zwei-dimensionaler Modellrechnung entsprechen die Ergebnisse den über die Wassertiefe gemittelten Werten.
Veröffentlichungen
- Casulli, V. (2008), A high-resolution wetting and drying algorithm for free-surface hydrodynamics, International Journal for Numerical Methods in Fluids, Volume 60, Issue 4, pages 391 - 408. See abstract.
- Casulli, V. and Stelling, G. S. (2010), Semi-implicit sub grid modelling of three-dimensional free-surface flows, International Journal for Numerical Methods in Fluids. See abstract.
- Sehili, A., Lang, G. and Lippert, C. (2014), High-resolution subgrid models: background, grid generation, and implementation, Ocean Dynamics, Volume 64, Issue 4, pages 519 - 535. See abstract.
Vorträge
- IZW-Campus (Podcast)
- 2020-06-16: UnTRIM - UnTRIM und seine Vorgänger.
- Neuester Vortrag:
- Neue Möglichkeiten in der Ästuarmodellierung, Vortragsfolien vom 22. September 2011, ca. 3.7 MB.
- Gittergenerierung für UnTRIM2, Vortragsfolien vom 22. September 2011, ca. 4.1 MB.
- Ältere Vorträge:
- An Overview of the Numerical Method within UnTRIM, Vortragsfolien vom 23. August 2011, ca. 1.2 MB.
- An Overview of the Numerical Method within UnTRIM2, Vortragsfolien vom 24. August 2011, ca. 1.8 MB.
- Further Experiences using Sub Grid Technology, Vortragsfolien vom 10. Mai 2011, ca. 11 MB.
- UNTRIM2 (sub grid) at BAW Hamburg, Vortragsfolien vom 11. November 2010, ca. 15 MB.
FuE-Projekte
- UnTRIM SubGrid-Topografie (2009-2011)
- Abschlussbericht, ca. 4.3 MB.
Weitere Anwender
Verschiedene Versionen des von Herrn Prof. Casulli bereit gestellten Berechnungskerns UnTRIM2 werden von folgenden Institutionen verwendet:
- Delta Modeling Associates, Inc., San Francisco, California, USA
- Resource Management Associates, Fairfield, California, USA
- University of California, Davis, California, USA
- Virginia Institute of Marine Science, Gloucester Point, Maryland, USA
Weitere Software
Vergleichbare Software (mit SubGrid-Technologie) ist derzeit nicht bekannt.
Validierungsdokument
Derzeit nicht verfügbar.
Benutzer-Schnittstellen-Beschreibung
Dieses Dokument enthält eine detaillierte Beschreibung aller dem Anwender des Simulationsverfahrens zur Verfügung stehenden Schnittstellen-Funktionen. Folgende Schnittstellen-Themen werden behandelt:
- Setzen von Daten (set-interfaces),
- Holen von Daten (get-interfaces),
- Testen des Gitters und der Genauigkeit der iterativ berechneten Lösung (check-routines),
- vom Berechnungskern gerufene externe Routinen (user-interface-routines) zum,
- Definieren der Namen der Dateien mit den Standard-Eingabedaten, zum
- Setzen des Anfangszustands, zum
- Setzen der Randwerte für jeden Berechnungszeitschritt, und zum
- Holen der Berechnungsergebnisse.
- tabellarische Aufzählung aller SET- und GET-Schnittstellen,
- Beispiele zu den Dateien mit den Standard-Eingabedaten.
Die PDF-Version der englischen Dokument-Fassung kann frei heruntergeladen werden:
- Neueste Version:
- UNTRIM2 (edition 2010) user interface description (in Englisch, ca. 740 kB)
- Ältere Versionen:
- UNTRIM2 (edition 2009) user interface description (in Englisch, ca. 1.4 MB)
MPI-Parallelisierung
Derzeit nicht realisiert.
BAW-spezifische Informationen
Gitternetzgenerierung
Für das Erzeugen des von UNTRIM2 benötigten unstrukturierten orthogonalen Gitters mit SubGrid-Bathymetrie wird der Gitternetz-Generator JANET eingesetzt, eine Entwicklung der Firma SmileConsult. Weitere Informationen zur Einbindung von JANET bei der BAW finden sich auf dem entsprechenden JANET-Programmkennblatt.
Simulation
Das mathematische Verfahren UNTRIM2 ist derzeit nur unvollständig in die Softwareumgebung der BAW eingebunden. Weitere Detailinformationen finden sich auf dem UNTRIM2-Programmkennblatt.
Grafische Darstellung der Berechnungsergebnisse
Für die grafische Darstellung der von UNTRIM2 erzeugten Ergebnisse stehen mehrere Methoden bereit. Zu den wichtigsten zählen,
- NCPLOT für flächenhaft vorliegende Daten,
- VVIEW2D und/oder LQ2PRO, für auf Quer- und Längsschnitten vorliegende Daten, sowie
- GVIEW2D, für an Einzelpositionen vorliegende Daten,
- QUICKPLOT für flächenhaft vorliegende Daten.
Analyse der Berechnungsergebnisse
Für eine Analyse der Berechnungsergebnisse stehen verschiedene Methoden für unterschiedlichste Fragestellungen bereit:
- NCANALYSE für die Berechnung verschiedener Kenngrößen (tideabhängig und tideunabhängig).
Kopplung mit weiteren Sub-Modellen
Derzeit nicht realisiert.
zurück zu Modellverfahren für den Küstenbereich und Ästuare
