Harmonic Analysis of Water Level

• General Information
• Main Constituents of Tides
• Shallow Water Constituents of Tides
• Tidal Harmonic Analysis
• Fortnightly (Phase) Inequality
• Diurnal Inequality
• Motivation to Perform a Tidal Harmonic Analysis
• Short Tide Glossary
• References

General Information

The tide is caused by the attraction of the Sun and the Moon on the oceans, and the rotation of the Earth. The precise pattern at any particular spot along the coast depends strongly on the shape of the coastline and on the profile of the seafloor nearby. Furthermore, in shallow seas, bays and estuaries co-oscillating tides and resonance contribute to a large amount to the final shape of the tides. The tides at any specific location are essentially impossible to calculate theoretically even though the generating gravitational forces are very precisely known.

This figure shows the tidal record for two weeks (January 1-14, 1884) at Bombay. The tide was recorded on a cylindrical sheet that turned once every 24 hours. Each daily curve is labelled with its date. Some obvious features: there are usually two high tides and two low tides each day; the tides come about 50 minutes later each day; during the two-week period there is considerable variation in the daily pattern of highs and lows; there is usually a difference in height between two consecutive high tides (the fortnightly (phase) inequality and the diurnal inequality). Note that in this graph, time increases to the left. From: Sir George Herbert DARWIN, Tides, in Encyclopaedia Britannica, R. S. Peale & Co. Chicago 1890 Vol. XXIII 353-381.

The fundamental frequencies for gravitational tides are related to the following astronomical time constants (MSD = mean solar day):

mean lunar day T1: The time of the rotation of the Earth with respect to the Moon, or the interval between two successive upper transits of the Moon over the meridian of a place. The mean lunar day is approximately 1.035050 MSD long. tropical month s: The average period of the revolution of the Moon around the Earth with respect to the vernal equinox. Its length is approximately 27.321582 MSD. tropical year h: The average period of the revolution of the Earth around the Sun with respect to the vernal equinox. Its length is approximately 365.2422 MSD. rotation of Moons perigee p: Change (as of January 1, 1900) in mean longitude of lunar perigee (period: 8.85 years). rotation of Moons node N: Change (as of January 1, 1900) in mean longitude of the Moon's node. (period: 18.61 years). rotation of Earths perigee p1: Change (as of January 1, 1900) in mean longitude of solar perigee (period: 20900 years).

An infinite number of harmonics and linear combinations of the fundamental frequencies can be observed in tidal signals. The Earths rotation causes a doubling of the frequencies which is related to the presence of two tidal bulges travelling around the world (a simplified view). Due to the large differences in the periods of the fundamental frequencies tides do contain usually also very close lying frequencies which are responsible for modulations of the range of the tides (e.g. the spring neap cycle).

Generation of tides

Freezed frame from the animation Entstehung der Gezeiten (in German), see accompanying link next to Animation.

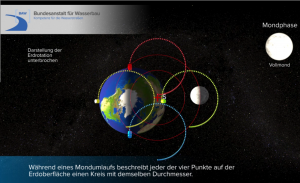
Gravitational as well as centrifugal forces cause tidal forces on Earth. Some significant causes as well as phenomena are explained in the following animation as well as on the poster:

• animation Entstehung der Gezeiten (in German, 325 MB, MP4 file format), and
• poster Gezeiten - Entstehung und Phänomene (in German, 18 MB, PDF file format).

You can find more of BAWs videos on AV-Portal TIB in Hannover (search there for BAW). All videos are marked using a Digital Object Identifier (DOI). Therefore videos can be as easily cited as common text publications. DOI for this video is http://dx.doi.org/10.5446/15182.

Main Constituents of Tides

Any main constituent of the tides is written using a capital letter and an index number which is appended to it. Index numbers 1 and 2 make it easy to distinguish between diurnal and semidiurnal tides. For example the M2-tide is the principal semidiurnal lunar constituent. Low frequencies are marked in a different way (e.g. f, mf, sa).

table with selected main constituents of tides
Abbreviation	Composition	Character
Ssa	2h	semiannual tide
Mm	s - p	monthly tide
Mf	2s	fortnightly tide
Q1	T1 - 2s + p	diurnal tide
O1	T1 - s	diurnal tide
P1	T1 + s - 2h	diurnal tide
K1	T1 + s	diurnal tide
N2	2T1 - s + p	semidiurnal tide
M2	2T1	semidiurnal tide
L2	2T1 + s - p	semidiurnal tide
S2	2T1 + 2s + 2h	semidiurnal tide
K2	2T1 + 2s	semidiurnal tide

The main constituents which are shown in this table are a combined result of multiplication, addition and subtraction of the fundamental frequencies. E.g. the frequency of the constituent Mm is obtained by subtracting the frequency of p from the frequency of s.

Shallow Water Constituents of Tides

Besides the astronomically dominated main constituents in shallow marginal or coastal seas additional frequencies do occur. The shallow water constituents are also called compound tides and overtides. They are mainly a results of the nonlinear dynamic processes which are present in the physics governing the motion of water, namely

1. dependence of the celerity of a tidal wave on the actual water depth;
2. nonlinear bottom friction;
3. advection of momentum.

Graphical representation of the asymmetric effects of nonlinear processes on a progressive tidal wave (with German text only). This graphical representation is also available in Encapsulated PostScript format.

Graphical representation of the symmetric effects of nonlinear processes on a progressive tidal wave (with German text only). This graphical representation is also available in Encapsulated PostScript format.

Graphical representation of the influence of river flow on dissipation (with German text only). This graphical representation is also available in Encapsulated PostScript format. The shallow water constituents are described using a combination of numbers and letters which are indicating the composition (linear combination of one or more main constituents) and frequency of the constituent.

The following table gives an overview over the most significant shallow water constituents of tides and their composition (e.g. compund tides like MSN2 or overtides like M4 and S4).

table with selected shallow water constituents of tides
Abbreviation	Composition	Character
MP1	M2 - P1	diurnal tide
SO1	S2 - O1	diurnal tide
MNS2	M2 + N2 - S2	semidiurnal tide
2MS2	2M2 - S2	semidiurnal tide
MSN2	M2 + S2 - N2	semidiurnal tide
2SM2	2S2 - M2	semidiurnal tide
MO3	M2 + O1	terdiurnal tide
MK3	M2 + K1	terdiurnal tide
MN4	M2 + N2	fourth diurnal tide
M4	2M2	fourth diurnal tide
MS4	M2 + S2	fourth diurnal tide
MK4	M2 + K2	fourth diurnal tide
S4	S2 + S2	fourth diurnal tide
M6	3M2	sixth diurnal tide
2MS6	2M2 + S2	sixth diurnal tide
M8	4M2	eighth diurnal tide

Tidal Harmonic Analysis

For any spot along the coast or in the open sea only the periods or frequencies of the constituents of the tides are known. Amplitude as well as phase are not known a priori. Measured tidal records as well as results from numerical siumulations can be used to determine amplitude and phase. This procedure is called Tidal Harmonic Analysis. Normally long tidal records are needed to determine amplitude and phase for a larger number of constituents with high accuracy. If we know amplitudes und phase of the tidal constituents at a specific location we can perform a forecast of sea level with a Tidal Harmonic Synthesis, a summation of all known constituents.

The Tide Predicter was designed in 1873 by Kelvin, based on a suggestion of Beauchamp Tower's for summing several trigonometric functions with independent periods. This machine was exhibited at the South Kensington Museum in 1876. It is designed to sum the M2, S2, N2, K1, O1, K2, L2, P1, M4 and MS4 constituents, in that order reading from the left. See also: KELVIN (= Sir William Thomson, Baron Kelvin), The tidal gauge, tidal harmonic analyser, and tide predicter, in Kelvin, Mathematical and Physical Papers (Volume VI), Cambridge 1911, pp 272-305. [From the Minutes of the Proceedings of the Institution of Civil Engineers, March 11, 1882.]

Fortnightly (Phase) Inequality

Variations in the tides or tidal currents due to changes in the phase of the Moon. At the times of new and full Moon the tide-producing forces of the Moon and Sun act in conjunction, causing the range of tide and speed of the tidal current to be greater than the average, the tides at these times being known as spring tides. At the times of the quadratures of the Moon these forces are opposed to each other, causing neap tides with diminished range and current speed.

Normally the amplitude of the S2-tideis mainly responsible for the differences between neap range and spring range.

The time interval between new or full Moon and the maximum effect of these phases upon range of tide or speed of the tidal current is called age of phase inequality. This age may be computed from the harmonic constants for M2 und S2.

Diurnal Inequality

The difference in height of the two high waters or of the two low waters of each tidal day is called diurnal inequality; also, the difference in speed between the two flood tidal currents or the two ebb currents of each tidal day. The difference changes with the declination of the Moon and, to a lesser extent, with the declination of the Sun. In general, the inequality tends to increase with increasing declination, either north or south, and to diminish as the Moon approaches the Equator.

The amplitudes of the constituents M2, S2, K1 and O1 can be used to calculate the form ratio F = (K1 + O1)/(M2 + S2) which leads to the following subdivisions:

F = 0.00 - 0.25:semidiurnal tides
F = 0.25 - 1.50:mixed, dominantly semidiurnal tides
F = 1.50 - 3.00:mixed, dominantly diurnal tides
F > 3.00:diurnal tides

Motivation to Perform a Tidal Harmonic Analysis

The calculation and graphic display of amplitude and phase for a reasonable number of tidal constituents contributes to a large amount for an improved understanding of the tide induced dynamic processes in coastal seas and estuaries.

• A comparison between tide records and numerically calculated results (see also mathematical models) can be made based on amplitudes and phases derived by means of a tidal harmonic analysis for a reasonable number of tidal constituents. This is a nice instrument in the verification process of a numerical model for a specific area. Deviations in amplitude and phase can be precisely quantified.
• Spatial variations of the tidal spectrum within an area of investigation are caused by topographic effects, nonlinear physical processes, resonance and reflexion. The interpretation of the spatial variations can be used to identify single processes and may contribute to an improved understanding of the natural system.
• Changes in relative phase and amplitude ratio between two constituents (e.g. between the M2-constituent and the corresponding overtides M4, M6 and M8) can be related to the asymmetry of the tide. Very often residual processes of water-, salt- and sediment-transport are closely linked to hydrodynamic asymmetries. Relationships between transport and hydrodynamic processes can be claryfied.

Graphical representation of superposition of M2 and M4 tide (with German text only). This graphical representation is also available in Encapsulated PostScript format

Graphical representation of superposition of M2 and M6 tide (with German text only). This graphical representation is also available in Encapsulated PostScript format.

Graphical representation of superposition of M2 and M4 or M6 tide in situations where double high- or low-waters occur (with German text only). This graphical representation is also available in Encapsulated PostScript format.

An automatic tidal harmonic analysis for the above shown constituents is carried through by the computer programs FRQWF and NCANALYSE. A tidal harmonic synthesis at single stations is done by the computer program FRQ2ZEITR.

Computational results of a tidal harmonic analysis

The Least Square Fit Method (LSQF) is used to perform a tidal harmonic analysis. Within programs FRQWF and NCANALYSE different routines of the software package LAPACK are used for this purpose.

For any tidal constituent the following quantities are computed.

Amplitude

Amplitude of a tidal constituent.
No example figures available yet.
Analysis programs: FRQWF and NCANALYSE.

Phase

Phase of a tidal constituent.
No example figures available yet.
Analysis programs: FRQWF and NCANALYSE.

Amplitude error

Error with respect to amplitude of a tidal constituent computed using the LSQF method.
No example figures available yet.
Analysis program: NCANALYSE.

Phase error

Error with respect to phase of a tidal constituent computed using the LSQF method.
No example figures available yet.
Analysis program: NCANALYSE.

Amplification of amplitude

Amplification of amplitude of a tidal constituent with respect to the amplitude computed at a reference location.
No example figures available yet.
Analysis program: NCANALYSE.

Phase difference

Difference of phase of a tidal constituent with respect to the phase computed at a reference location.
No example figures available yet.
Analysis program: NCANALYSE.

Short Tide Glossary

Ssa-constituent: Solar semiannual constituent. This constituent, with Sa, accounts for the nonuniform changes in the Sun's declination and distance. In actuality, they mostly reflect yearly meteorological variations influencing sea level.

Mm-constituent: Lunar monthly constituent. This constituent expresses the effect of irregularities in the Moon's rate of change of distance and speed in orbit.

Mf-constituent: Lunar fort nightly constituent. This constituent expresses the effect of departure from a sinusoidal declinational motion.

O1-constituent: Lunar diurnal constituent. See K1.

Q1-constituent: Larger lunar elliptic diurnal constituent. This constituent modulates the amplitude and frequency of the declinational O1.

K1-constituent: Lunisolar diurnal constituent. This constituent, with O1, expresses the effect of the Moon's declination. They account for diurnal inequality and, at extremes, diurnal tides. With P1, it expresses the effect of the Sun's declination.

P1-constituent: Solar diurnal constituent. See K1.

L2-constituent: Smaller lunar elliptic semi diurnal constituent. This constituent, with N2, modulates the amplitude and frequency of M2 for the effect of variation in the Moon's oribital speed due to its elliptical orbit.

N2-constituent: Larger lunar elliptic semi diurnal constituent. See L2.

M2-constituent: Principal lunar semidiurnal constituent. This constituent represents the rotation of the Earth with respect to the Moon.

S2-constituent: Principal solar semi diurnal constituent. This constituent represents the rotation of the Earth with respect to the Sun.

K2-constituent: Lunisolar semi diurnal constituent. This constituent modulates the amplitude and frequency of M2 and S2 for the declinational effect of the Moon and Sun, respectively.

References

DEFANT, 1953

Albert Defant, 1953, Ebbe und Flut des Meeres, der Atmosphäre und der Erdfeste, Springer Verlag.

DIETRICH et al., 1975

G. Dietrich, K. Kalle, W. Krauss, G. Siedler, 1975, Allgemeine Meereskunde, Kap. 9: Gezeitenerscheinungen, (in German language), 3. Auflage, Gebr. Bornträger.

DHI, 1967

Deutsches Hydrographisches Institut, 1967, Tafeln der astronomischen Argumente V0 + v und der Korrektionen j, v zum Gebrauch bei der harmonischen Analyse und Vorausberechnung der Gezeiten für die Jahre 1900 bis 1999, (in German language), DHI Nr. 2276.

Horn, 1948

W. Horn, 1948, Über die Darstellung der Gezeiten als Funktion der Zeit, (in German language), German Hydrogr. Journal 1, no. 4.

PUGH, 1987

David T. Pugh, 1987, Tides, Surges and Mean Sea Level, John Wiley and Sons.

---

back to Analysis of Calculated Results

---

Overview