Systematic studies for recording squat and trim together with ship-induced pressure and wave systems when passing through channels in confined shallow water
From BAWiki
Author: K. Uliczka
Boundary conditions
The studies into the dynamic behaviour of very large Post-Panamax container ships when passing through waterways of confined width and depth were conducted in BAW-DH’s shallow water basin (length approx. 100 m, width approx. 35 m, max. water depth 0.7 m) at 1:40 scale in accordance with Froude’s model laws.
The dimensions and investigated parameters for the model ships used were as follows:
| Designation | Length | Beam | Draught | UKCR* | cB-value** | SR+ | Weight trim | KG++ |
| - | m | m | m | m | - | - | - | m |
| JUMBO | 320 | 40 | 14,5 | 1-2 | 0,740 | 6,29 | Hard | 11,8 |
| MEGA-JUMBO | 360 | 55 | 15,5 | 1-1,5-2 | 0,677 | 6,10 | Hard | 10,2 |
*UKCR: under-keel-clearance, **cB: block coefficient , +SR: slenderness ratio, ++KG: centre of gravity above keel
The Froude numbers amounted to 0,27 < Frh < 0,68. The Reynolds numbers were determined to be 3,1 · 106 < Re < 6,2 · 107 (factor 10 > ReKRIT,erf). Fulfilling the geometric and dynamic similarity conditions ensured that the studies would deliver valid forecasts.
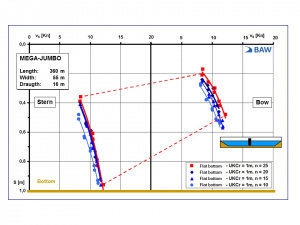
The waterway cross-sections and (partial-)cross-sectional ratios are presented in Figure 1 taking the MEGA-JUMBO as an example:
- Trapezoidal profile, central course, cross-sectional ratios n = 25, 20, 15, 10 (Results of CFD-Simulations).
- Trapezoidal profile, off-centre course, partial cross-sectional ratios nT = 10/5, 20/10, 25/10.
- Combined profile, off-centre course, partial-cross-sectional ratios nT = 25/10, 20/10, 10/5.

Comments:
Cross-sectional ratio n = A / AS
where: A wetted area of waterway
AS submerged midship cross-section
Partial-cross-sectional ratio nT = AT / 0,5 AS
where: AT area of wetted partial-cross-section (from course to bank)
As well as measuring ship dynamics (squat, trim), the speed-dependent changes in the water level in a transverse profile were also assessed and analysed. Selected results are presented and evaluated below.
Selected results – squat and trim
The following relationships have been identified, taking the MEGA-JUMBO measurement results as an example:
- Smaller cross-sectional ratios between the submerged midship cross-section and the wetted cross-section mean higher speed-dependent squat values (Figure 2).
- Various waterway ratios relating to shape and width, from infinite to narrow waterway widths and down to fairways in shallow open water lead to a marked increase in squat (Figure 3).
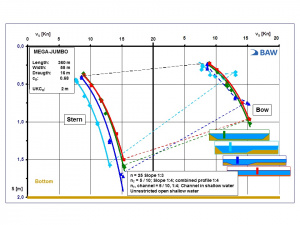
The results of the extensive studies demonstrate that both fairway depth and waterway width (i.e. the cross-section of the waterway construction) must be factored into the preliminary calculation of maximum speed- and vessel-dependent squat, particularly in longer approach channels to major seaports such as the tidal Elbe, the tidal Weser or the Schelde flowing into the port of Antwerp, in order for the WSV to guarantee ease and safe shipping to seaports.
Selected results – ship-generated load
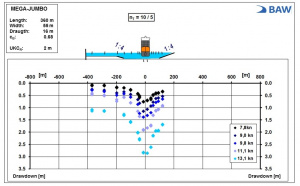
The changes in water level measured at the same time as ship dynamics (drawdown zA, primary wave HP and secondary wave HS) as well as their cross-section-dependent distribution within the waterway are shown in Figures 4 and 5, taking the drawdown zA as an example:
- A central course generates a symmetrical distribution and decrease in speed-dependent drawdown in the waterway cross-section (Figure 4, central course, left-hand side).
- At low UKC values, the partial-cross-sectional ratio determines the decrease in drawdown towards the bank (Figure 4, off-centre course, right-hand side).
- Comparing the two charts in Figure 4 highlights the decrease in drawdown in the waterway cross-section that depends on the passing clearance between ship and bank: on the right-hand bank, the drawdown load is virtually the same as the partial-cross-sectional ratios are similar. On the left-hand bank, however, the larger passing clearance of the moving ship means a much lower load at the foot of the embankment.

- If the cross-sectional ratios are very narrow, even much lower ship speeds (in this case vS,MAX = 13,1 kn) can generate high loads on the bank (Figure 5, central course within a fairway in an asymmetrical waterway).
A more detailed analysis of the long-period ship-generated loads that apply at the toe of slope and that depend on the partial-cross-sections (in this case the drawdown zA) summarises the results from the BAW’s extensive system tests for the JUMBO container ship (PPM40) in Figure 6. The chart illustrates the decrease functions for the drawdown zA depending on the partial cross-sectional ratio nT for a PPM40 container ship travelling at various speeds.
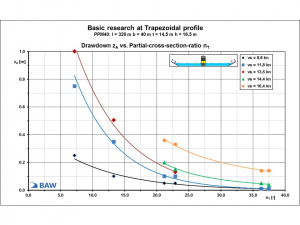
For example, the decrease function for a PPM40 ship travelling at around vS ≈ 13,5 kn (Figure 6, red curve) can be used to predict that partial-cross-sectional ratios of between 10 < nT < 23 23 will give rise to a load decrease with a factor of about F ≈ 5.
The speed-dependent trend lines also highlight the lack of any linear relationship between long-period ship-generated load and partial-cross-sectional ratio.
Conclusions
- In terms of squat size, both under-keel clearance UKCR as well as the cross-sectional ratio n between the submerged midship cross-section AS zand the wetted cross-section A (S = f (n, UKCR, vS, ...) with n = AS / A) should be taken into account when design fairway depth.
- An off-centre course only results in low to minimal increases in squat compared to a central course (S ≠ f (L, ...) ).
- Neither the shape of the embankment nor the foreshore area had a significant observable impact on squat assuming the same waterway cross-section (S ≠ f (1:m, …) ).
- If the UKCR is low, the partial-cross-sectional ratio nT of ship AS/2 2 and wetted partial-area AT will determine the speed-dependent element of the long-period ship-generated wave and flow load (e.g.: drawdown zA = f (nT, vS, …) with nT = 0,5 AT / AS at AT = f (L, ...) ).
zurück zu Ship Dynamics
