Mathematical Methods: Difference between revisions
From BAWiki
imported>Seiss Guntram m simulation methods added in listing |
The LinkTitles extension automatically added links to existing pages (<a target="_blank" rel="nofollow noreferrer noopener" class="external free" href="https://github.com/bovender/LinkTitles">https://github.com/bovender/LinkTitles</a>). |
||
| (5 intermediate revisions by one other user not shown) | |||
| Line 1: | Line 1: | ||
[[de:Mathematische Verfahren]] | [[de:Mathematische Verfahren]] | ||
[[File: Methoden_mathematische_Verfahren.jpg|thumb|Picture 1: Numerics]] | [[File: Methoden_mathematische_Verfahren.jpg|240px|thumb|Picture 1: Numerics]] | ||
[[File: Methoden_mathematische_Verfahren2.jpg|210px|thumb|Picture 2: Three-dimensional numerical calculation of the velocity distributions in a river bend.]] | |||
Mathematical methods can be used to obtain results about natural processes (simulation). They also permit predictions of natural developments and the impact of anthropogenic intervention in natural systems. The central [[Simulation Methods|simulation methods]] are supplemented by methods of data processing and grid generation ([[Pre- and Postprocessing|preprocessing]]), as well as visualizing and analysing the calculation results ([[Pre- and Postprocessing|postprocessing]]). | Mathematical methods can be used to obtain results about natural processes (simulation). They also permit predictions of natural developments and the impact of anthropogenic intervention in natural systems. The central [[Simulation Methods|simulation methods]] are supplemented by methods of data processing and grid generation ([[Pre- and Postprocessing|preprocessing]]), as well as visualizing and analysing the calculation results ([[Pre- and Postprocessing|postprocessing]]). | ||
Before using a mathematical method, the natural system has to be analysed with regard to the processes involved. With a view to the system in question, e.g. river or estuary, and the issue at stake, a choice has to be made in terms of the processes that the model has to consider (model functionality). This is the basis for formulating the conceptual model, usually in the form of ordinary or partial differential equations. As a rule, it is not possible to solve these exactly when natural systems are involved. Individual processes such as bed friction can only be considered in a simplified form (parameter configuration). In addition, the unknown variables (water level, current velocity etc.) can only be calculated at a finitely large number of places and dates (discretization). The fundamental equations and assumptions for discretization and parameter configuration lead to the algorithmic implementation of the model using numerical mathematical methods. This is then followed by software implementation that is verified using basic examples. The result is a mathematical method with limited validity that can be used for simulation of various site-specific models (river Rhine near Bingen, tidal Elbe, etc.) Different mathematical methods can be used at the BAW for a wide range of natural processes. | Before using a mathematical method, the natural system has to be analysed with regard to the processes involved. With a view to the system in question, e.g. river or [[estuary]], and the issue at stake, a choice has to be made in terms of the processes that the [[model]] has to consider ([[model]] functionality). This is the basis for formulating the conceptual [[model]], usually in the form of ordinary or partial differential equations. As a rule, it is not possible to solve these exactly when natural systems are involved. Individual processes such as bed friction can only be considered in a simplified form (parameter configuration). In addition, the unknown variables ([[water level]], current velocity etc.) can only be calculated at a finitely large number of places and dates (discretization). The fundamental equations and assumptions for discretization and parameter configuration lead to the algorithmic implementation of the [[model]] using numerical mathematical methods. This is then followed by software implementation that is verified using basic examples. The result is a mathematical method with limited validity that can be used for simulation of various site-specific models (river Rhine near Bingen, [[tidal Elbe]], etc.) Different mathematical methods can be used at the BAW for a wide range of natural processes. | ||
Preprocessing entails generating initial and boundary values for the entire simulation period as well as the computation grid for the corresponding site-specific model. Later on, the consistent computational results of a simulation are compared with observation data (calibration, validation), visualized in graphic terms, turned into animations to clarify dynamic processes or subjected to further analysis for calculating characteristic parameters (e.g. high-tide, maximum current velocity) and their change (prediction). | Preprocessing entails generating initial and boundary values for the entire simulation period as well as the computation grid for the corresponding site-specific [[model]]. Later on, the consistent computational results of a simulation are compared with observation data ([[calibration]], validation), visualized in graphic terms, turned into animations to clarify dynamic processes or subjected to further analysis for calculating characteristic parameters (e.g. high-tide, maximum current velocity) and their change (prediction). | ||
==Documentations== | ==Documentations== | ||
Latest revision as of 09:12, 21 October 2022
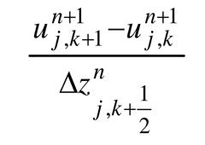
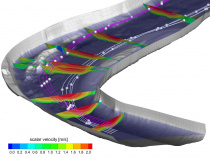
Mathematical methods can be used to obtain results about natural processes (simulation). They also permit predictions of natural developments and the impact of anthropogenic intervention in natural systems. The central simulation methods are supplemented by methods of data processing and grid generation (preprocessing), as well as visualizing and analysing the calculation results (postprocessing).
Before using a mathematical method, the natural system has to be analysed with regard to the processes involved. With a view to the system in question, e.g. river or estuary, and the issue at stake, a choice has to be made in terms of the processes that the model has to consider (model functionality). This is the basis for formulating the conceptual model, usually in the form of ordinary or partial differential equations. As a rule, it is not possible to solve these exactly when natural systems are involved. Individual processes such as bed friction can only be considered in a simplified form (parameter configuration). In addition, the unknown variables (water level, current velocity etc.) can only be calculated at a finitely large number of places and dates (discretization). The fundamental equations and assumptions for discretization and parameter configuration lead to the algorithmic implementation of the model using numerical mathematical methods. This is then followed by software implementation that is verified using basic examples. The result is a mathematical method with limited validity that can be used for simulation of various site-specific models (river Rhine near Bingen, tidal Elbe, etc.) Different mathematical methods can be used at the BAW for a wide range of natural processes.
Preprocessing entails generating initial and boundary values for the entire simulation period as well as the computation grid for the corresponding site-specific model. Later on, the consistent computational results of a simulation are compared with observation data (calibration, validation), visualized in graphic terms, turned into animations to clarify dynamic processes or subjected to further analysis for calculating characteristic parameters (e.g. high-tide, maximum current velocity) and their change (prediction).
Documentations
Validation Studies
back to: Hydraulic Engineering Methods
