Analytical and Empirical Methods: Difference between revisions
From BAWiki
imported>Spohr Susanne Created page with 'de:Analytische und empirische Ansätze ==Traditional Methods== thumb|Graph 1: spectrum of possible calculated results Whereas analytical derivations …' |
The LinkTitles extension automatically added links to existing pages (<a target="_blank" rel="nofollow noreferrer noopener" class="external free" href="https://github.com/bovender/LinkTitles">https://github.com/bovender/LinkTitles</a>). |
||
| Line 3: | Line 3: | ||
[[File: Seb.Bild3.jpg|thumb|Graph 1: spectrum of possible calculated results]] | [[File: Seb.Bild3.jpg|thumb|Graph 1: spectrum of possible calculated results]] | ||
Whereas analytical derivations can be used for the calculation of the water level depression z<sub>A</sub> (e.g. KREY, 1913; CONSTANTINE, 1960; BOUWMEESTER et al., 1977; FÜHRBÖTER, 1982), the calculation methods for determining the wave heights of ship waves, often aided by model studies and/or field measurements, are empirical (e.g., RÖMISCH, 1969). Though the short period secondary waves are taken into account by some of the empirical approaches, they are not known in detail as functions of the described parameters. This is because these secondary waves are generated as a function of ship speed and ship form and as a result of the different pressure distributions along the body of the ship. | Whereas analytical derivations can be used for the calculation of the [[water level]] depression z<sub>A</sub> (e.g. KREY, 1913; CONSTANTINE, 1960; BOUWMEESTER et al., 1977; FÜHRBÖTER, 1982), the calculation methods for determining the wave heights of ship waves, often aided by [[model]] studies and/or field measurements, are empirical (e.g., RÖMISCH, 1969). Though the short period [[secondary waves]] are taken into account by some of the empirical approaches, they are not known in detail as functions of the described parameters. This is because these [[secondary waves]] are generated as a function of ship speed and ship form and as a result of the different pressure distributions along the body of the ship. | ||
The following simplified relationships have been culled from the literature for the subcritical speed range (i.e., v<sub>S</sub> < 0.9·[g·d]<sup>0.5</sup>).This is the range used, for economical reasons, by merchant shipping:<br /> | The following simplified relationships have been culled from the literature for the subcritical speed range (i.e., v<sub>S</sub> < 0.9·[g·d]<sup>0.5</sup>).This is the range used, for economical reasons, by merchant shipping:<br /> | ||
* water level depression and wave height<br />z<sub>A</sub> proportional to v<sub>S</sub><sup>k</sup> with 2 < k < 3.5 <br />z<sub>A</sub> proportional to n<sup>k</sup> with -1.5 < k < -1 | * [[water level]] depression and wave height<br />z<sub>A</sub> proportional to v<sub>S</sub><sup>k</sup> with 2 < k < 3.5 <br />z<sub>A</sub> proportional to n<sup>k</sup> with -1.5 < k < -1 | ||
* return current velocity<br />v<sub>R</sub> proportional to v<sub>S</sub> <br />v<sub>R</sub> proportional to n<sup>-1</sup> | * return current velocity<br />v<sub>R</sub> proportional to v<sub>S</sub> <br />v<sub>R</sub> proportional to n<sup>-1</sup> | ||
<br /> | <br /> | ||
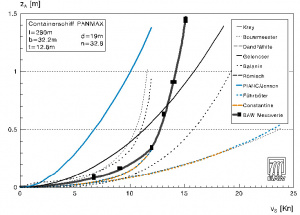
The diagram (Graph 1) shows the spectrum of possible calculated results given the boundary conditions at a cross-section of the Lower Elbe compared to the measurement data won from a hydraulic model of the BAW-DH. | The diagram (Graph 1) shows the spectrum of possible calculated results given the boundary conditions at a [[cross-section]] of the Lower Elbe compared to the measurement data won from a hydraulic [[model]] of the BAW-DH. | ||
Not only is the interaction between ship and waterway critical for forming a prognosis on ship induced loading in waterways with varying non-uniform cross-sections, but also the physical processes of wave spreading such as refraction and shoaling are critical and must be accounted for in the calculations (without parameterization). | Not only is the interaction between ship and [[waterway]] critical for forming a prognosis on ship induced loading in waterways with varying non-uniform cross-sections, but also the physical processes of wave spreading such as refraction and [[shoaling]] are critical and must be accounted for in the calculations (without parameterization). | ||
Traditional empirical and analytical approaches only allow for an inadequate estimation of the ship induced loading caused by sea-going merchant shipping on large fairways with varying non-uniform cross-sectional geometries, especially in tidal regions. Thus these approaches are inadequate for calculating the magnitude of future loading on waterways. | Traditional empirical and analytical approaches only allow for an inadequate estimation of the ship induced loading caused by sea-going merchant shipping on large fairways with varying non-uniform cross-sectional geometries, especially in tidal regions. Thus these approaches are inadequate for calculating the magnitude of future loading on waterways. | ||
Latest revision as of 10:17, 21 October 2022
Traditional Methods
Whereas analytical derivations can be used for the calculation of the water level depression zA (e.g. KREY, 1913; CONSTANTINE, 1960; BOUWMEESTER et al., 1977; FÜHRBÖTER, 1982), the calculation methods for determining the wave heights of ship waves, often aided by model studies and/or field measurements, are empirical (e.g., RÖMISCH, 1969). Though the short period secondary waves are taken into account by some of the empirical approaches, they are not known in detail as functions of the described parameters. This is because these secondary waves are generated as a function of ship speed and ship form and as a result of the different pressure distributions along the body of the ship.
The following simplified relationships have been culled from the literature for the subcritical speed range (i.e., vS < 0.9·[g·d]0.5).This is the range used, for economical reasons, by merchant shipping:
- water level depression and wave height
zA proportional to vSk with 2 < k < 3.5
zA proportional to nk with -1.5 < k < -1
- return current velocity
vR proportional to vS
vR proportional to n-1
The diagram (Graph 1) shows the spectrum of possible calculated results given the boundary conditions at a cross-section of the Lower Elbe compared to the measurement data won from a hydraulic model of the BAW-DH.
Not only is the interaction between ship and waterway critical for forming a prognosis on ship induced loading in waterways with varying non-uniform cross-sections, but also the physical processes of wave spreading such as refraction and shoaling are critical and must be accounted for in the calculations (without parameterization).
Traditional empirical and analytical approaches only allow for an inadequate estimation of the ship induced loading caused by sea-going merchant shipping on large fairways with varying non-uniform cross-sectional geometries, especially in tidal regions. Thus these approaches are inadequate for calculating the magnitude of future loading on waterways.
back to Ship-generated Loading
