Analytical methods: Difference between revisions
From BAWiki
No edit summary |
The LinkTitles extension automatically added links to existing pages (<a target="_blank" rel="nofollow noreferrer noopener" class="external free" href="https://github.com/bovender/LinkTitles">https://github.com/bovender/LinkTitles</a>). |
||
| Line 2: | Line 2: | ||
[[File:05_Analytische_V_02.jpg|200px|thumb|right|Picture 2: Earth pressure failure mechanisms]] | [[File:05_Analytische_V_02.jpg|200px|thumb|right|Picture 2: Earth pressure failure mechanisms]] | ||
[[File:05_Analytische_V_03.jpg|200px|thumb|right|Picture 3: Ground failure diagram]]A well-known example is the concept of subgrade reaction approach which defines a bedding or subgrade reaction module to compute the interaction of the soil with the foundation plate. The approach is based on the assumption that the settlement is linearly dependent on the normal base pressure, whereupon the linear factor has the quality of a spring constant. The subgrade modulus can best be evaluated by assuming a simplified (linear) base pressure and performing a settlement calculation with then can be corrected iteratively. Despite these simplifications, the method offered for a long time the only available solution to deal with interaction analyses. Nowadays [[Numerical Methods|numerical methods]] are a readily available and a better way to calculate deformations for serviceability limit state design and to map the interaction between a structure and the soil. Analytical methods can also be used to observe time-dependent processes such as consolidation settlement and creep of fine-grained clayey and silty soils. | [[File:05_Analytische_V_03.jpg|200px|thumb|right|Picture 3: Ground failure diagram]]A well-known example is the concept of subgrade reaction approach which defines a bedding or subgrade reaction module to compute the interaction of the soil with the foundation plate. The approach is based on the assumption that the settlement is linearly dependent on the normal [[base]] pressure, whereupon the linear factor has the quality of a spring constant. The subgrade modulus can best be evaluated by assuming a simplified (linear) [[base]] pressure and performing a settlement calculation with then can be corrected iteratively. Despite these simplifications, the method offered for a long time the only available solution to deal with interaction analyses. Nowadays [[Numerical Methods|numerical methods]] are a readily available and a better way to calculate deformations for serviceability limit state design and to map the interaction between a structure and the soil. Analytical methods can also be used to observe time-dependent processes such as consolidation settlement and creep of fine-grained clayey and silty soils. | ||
Analysis of ultimate limit state comprises calculation of active or passive earth pressure which occurs when a wall is pushed against or moves away from the backfill, bearing resistance or punching failure of a foundation loaded by an excessive load or the loss of overall slope stability. Corresponding tasks are then defined by calculating the safety factor against ultimate limit state or failure of structural elements. The corresponding calculation methods are governed by standards. | Analysis of ultimate limit state comprises calculation of active or passive earth pressure which occurs when a wall is pushed against or moves away from the backfill, bearing resistance or punching failure of a foundation loaded by an excessive load or the loss of overall slope stability. Corresponding tasks are then defined by calculating the safety factor against ultimate limit state or failure of structural elements. The corresponding calculation methods are governed by standards. | ||
[[File:05_Analytische_V_04.jpg|200px|thumb|right|Picture 4: Embankment failure diagram]]The analytical methods for monitoring ultimate limit states are based on calculating the applicable load capacity (collapse load), which is done using collapse theorems from plasto-mechanics. The static or lower bound theorem states that a body will not fail if there is (at least) one permitted stress-field that fulfils the boundary and equilibrium conditions. The kinematic or upper bound theorem states that a base will collapse if there is a failure mechanism by which the external forces exceed the internal work being done to overcome the shear strength. Given that solutions based on the lower bound theorem limit the load capacity from the bottom up, the error is usually kept on the safe side. The kinematic theorem is used in the vast majority of actual cases as it is easier to apply. This involves studying an adequate number of kinematically feasible (rigid-plastic) failure mechanisms and thus determining which of these offers the least factor of safety. | [[File:05_Analytische_V_04.jpg|200px|thumb|right|Picture 4: Embankment failure diagram]]The analytical methods for [[monitoring]] ultimate limit states are based on calculating the applicable [[load capacity]] (collapse load), which is done using collapse theorems from plasto-mechanics. The static or lower bound theorem states that a body will not fail if there is (at least) one permitted stress-field that fulfils the boundary and equilibrium conditions. The kinematic or upper bound theorem states that a [[base]] will collapse if there is a failure mechanism by which the external forces exceed the internal work being done to overcome the shear strength. Given that solutions based on the lower bound theorem limit the [[load capacity]] from the bottom up, the error is usually kept on the safe side. The kinematic theorem is used in the vast majority of actual cases as it is easier to apply. This involves studying an adequate number of kinematically feasible (rigid-plastic) failure mechanisms and thus determining which of these offers the least factor of safety. | ||
Analytical methods for calculating groundwater flows are described on the following page. | Analytical methods for calculating groundwater flows are described on the following page. | ||
Latest revision as of 10:15, 21 October 2022
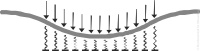
Analytical methods applied in conventional geotechnical engineering are often to calculate the vertical displacements of the subsoil (settlement and heave) and the behaviour of soil in its ultimate limit state.
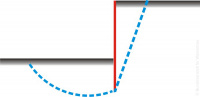

A well-known example is the concept of subgrade reaction approach which defines a bedding or subgrade reaction module to compute the interaction of the soil with the foundation plate. The approach is based on the assumption that the settlement is linearly dependent on the normal base pressure, whereupon the linear factor has the quality of a spring constant. The subgrade modulus can best be evaluated by assuming a simplified (linear) base pressure and performing a settlement calculation with then can be corrected iteratively. Despite these simplifications, the method offered for a long time the only available solution to deal with interaction analyses. Nowadays numerical methods are a readily available and a better way to calculate deformations for serviceability limit state design and to map the interaction between a structure and the soil. Analytical methods can also be used to observe time-dependent processes such as consolidation settlement and creep of fine-grained clayey and silty soils.
Analysis of ultimate limit state comprises calculation of active or passive earth pressure which occurs when a wall is pushed against or moves away from the backfill, bearing resistance or punching failure of a foundation loaded by an excessive load or the loss of overall slope stability. Corresponding tasks are then defined by calculating the safety factor against ultimate limit state or failure of structural elements. The corresponding calculation methods are governed by standards.
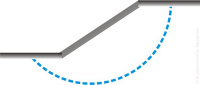
The analytical methods for monitoring ultimate limit states are based on calculating the applicable load capacity (collapse load), which is done using collapse theorems from plasto-mechanics. The static or lower bound theorem states that a body will not fail if there is (at least) one permitted stress-field that fulfils the boundary and equilibrium conditions. The kinematic or upper bound theorem states that a base will collapse if there is a failure mechanism by which the external forces exceed the internal work being done to overcome the shear strength. Given that solutions based on the lower bound theorem limit the load capacity from the bottom up, the error is usually kept on the safe side. The kinematic theorem is used in the vast majority of actual cases as it is easier to apply. This involves studying an adequate number of kinematically feasible (rigid-plastic) failure mechanisms and thus determining which of these offers the least factor of safety.
Analytical methods for calculating groundwater flows are described on the following page.
Analytical methods – Groundwater flow
back to: Geotechnical Engineering Methods
