Ship-generated Loading: Difference between revisions
From BAWiki
No edit summary |
The LinkTitles extension automatically added links to existing pages (<a target="_blank" rel="nofollow noreferrer noopener" class="external free" href="https://github.com/bovender/LinkTitles">https://github.com/bovender/LinkTitles</a>). |
||
| (10 intermediate revisions by one other user not shown) | |||
| Line 1: | Line 1: | ||
[[de:Schiffserzeugte Belastungen]] | [[de:Schiffserzeugte Belastungen]] | ||
The change in draught- and speed-related ship-induced loading on the shipping routes entails a definition of the characteristic parameters (e.g. ship wave system, displacement current) and requires knowledge of the functional relationships (e.g. ship speed and vessel width, shipping channel conditions, passing clearance). Picture 1 shows a diagram of the ship wave system among others. | The change in [[draught]]- and speed-related ship-induced loading on the shipping routes entails a [[Definition of the Characteristic Parameters|definition of the characteristic parameters]] (e.g. ship wave system, displacement current) and requires knowledge of the [[Functional Relationships|functional relationships]] (e.g. ship speed and vessel width, shipping [[channel]] conditions, passing clearance). Picture 1 shows a diagram of the ship wave system among others. | ||
Since the start of the new century, a large number of analytical and empirical methods have been developed for calculating the interaction of ship and waterway. Initial calculations with hydrodynamic-numerical models reveal deviations compared to the results of hydraulic scale models, so that these numerical models cannot yet be viewed as a confirmed scientific aid for determining upgrading-related changes to ship-induced loading in shipping channels. At the moment, it is only possible to make confirmed quantitative predictions of ship-induced loadings in inhomogeneous waterways by means of hydraulic model tests in a scientifically confirmed model scale (state-of-the-art engineering and science). | Since the start of the new century, a large number of [[Analytical and Empirical Methods|analytical and empirical methods]] have been developed for calculating the interaction of ship and [[waterway]]. Initial calculations with hydrodynamic-numerical models reveal deviations compared to the results of hydraulic scale models, so that these numerical models cannot yet be viewed as a confirmed scientific aid for determining upgrading-related changes to ship-induced loading in shipping channels. At the moment, it is only possible to make confirmed quantitative predictions of ship-induced loadings in inhomogeneous waterways by means of hydraulic [[model]] tests in a scientifically confirmed [[model]] scale (state-of-the-art engineering and science). | ||
In recent years, the BAW Hamburg office has looked at the issue of the interaction between seagoing ship and tidal fairways both with studies on hydraulic models and with field study measurements. | In recent years, the BAW Hamburg office has looked at the issue of the interaction between seagoing ship and tidal fairways both with studies on hydraulic models and with [[field study measurements]]. | ||
==Definition of the Characteristic Parameters== | |||
[[de:Definition der Kenngrößen]] | |||
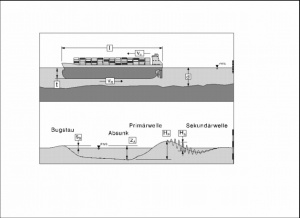
[[File: Seb.Bild2.jpg|thumb|Picture 1: Parameters and Functional Dependencies]] | |||
* [[ | A moving ship generates waves of different periods as a consequence of its displacement current causing pressure and [[water level]] changes at its bow, stern and alongside its hull. The following parameters describe the ship wave and current system, for example, for a ship moving in an [[estuary]] at subcritical speed (ship speed less than the phase speed of the prevailing waves): | ||
* [[Functional Relationships]] | * the bow pressure ('''s<sub>B</sub>''') directly at the hull, | ||
* [[ | * the [[water level]] depression ('''z<sub>A</sub>''') at the side of the ship, | ||
* [[ | * the stern wave ('''H<sub>P</sub>''') which is a part of the long period [[primary wave]] system, | ||
* the secondary wave superimposed on the [[primary wave]] system ('''H<sub>S</sub>'''), | |||
* velocity ('''v<sub>R</sub>''') of the simultaneously occurring return current. | |||
The [[water level]] changes for a depth- and width-limited [[waterway]], as seen by an observer from the [[bank]], are shown as a vertically exaggerated sideview in the above sketch. | |||
<br /> | |||
==Functional Relationships== | |||
[[de:Funktionelle Abhängigkeiten]] | |||
The parameters for the [[water level]] and current variations caused by a moving ship are a function of: | |||
* ship velocity '''v<sub>S</sub>''' and the passing distance '''L''' | |||
* ship dimensions (length '''l''', width '''b''', [[draught]] '''t''', submerged midship [[cross-section]] '''A<sub>S</sub>''') | |||
* total hydrodynamic resistance of the ship (ship form) in the canal '''R<sub>T,K</sub>''' | |||
* [[waterway]] conditions ([[water level]] '''B''' and bed width '''B<sub>S</sub>''', [[water depth]] '''d''', [[cross-section]] and area '''A''', [[bank]] profile and slope '''1 : m''') | |||
* current conditions in the [[waterway]] | |||
* other influences such as [[waterway]] bend, type of propulsion, water density. | |||
<br /> | <br /> | ||
The ''essential'' parameters for the ship induced loading for fairways have been shown to be: | |||
* the ship velocity ('''v<sub>S</sub>''') | |||
* the passing distance ('''L''') to the [[bank]] edge which defines the hydraulic partial [[cross-section]] ('''A<sub>T</sub>''') | |||
* the [[water depth]] to [[draught]] ratio ('''d/t'''), and the [[cross-section]] ratio '''A<sub>T</sub> / 0,5 A<sub>S</sub>'''. | |||
To illustrate more simply the physical processes occurring when a ship is moving in a [[waterway]] of varying non-uniform [[cross-section]], one may think of the [[waterway]] [[cross-section]] as being divided into two parts '''A<sub>T1</sub>''' and '''A<sub>T2</sub>''', through each of which half of the ship's displacement passes. Thus each [[bank]] experiences a qualitatively different ship induced loading as is determined by the partial [[cross-section]] ratios '''A<sub>T1</sub> / 0,5 A<sub>S</sub>''' and '''A<sub>T2</sub> / 0,5 A<sub>S</sub>'''. | |||
<br /> | |||
==Analytical and Empirical Methods== | |||
[[de:Analytische und empirische Ansätze]] | |||
===Traditional Methods=== | |||
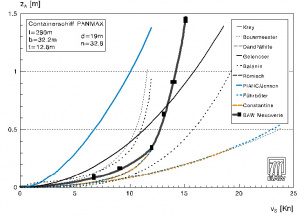
[[File: Seb.Bild3.jpg|thumb|Picture 1: spectrum of possible calculated results]] | |||
Whereas analytical derivations can be used for the calculation of the [[water level]] depression z<sub>A</sub> (e.g. KREY, 1913; CONSTANTINE, 1960; BOUWMEESTER et al., 1977; FÜHRBÖTER, 1982), the calculation methods for determining the wave heights of ship waves, often aided by [[model]] studies and/or field measurements, are empirical (e.g., RÖMISCH, 1969). Though the short period [[secondary waves]] are taken into account by some of the empirical approaches, they are not known in detail as functions of the described parameters. This is because these [[secondary waves]] are generated as a function of ship speed and ship form and as a result of the different pressure distributions along the body of the ship. | |||
The following simplified relationships have been culled from the literature for the subcritical speed range (i.e., v<sub>S</sub> < 0.9·[g·d]<sup>0.5</sup>).This is the range used, for economical reasons, by merchant shipping:<br /> | |||
* [[water level]] depression and wave height<br />z<sub>A</sub> proportional to v<sub>S</sub><sup>k</sup> with 2 < k < 3.5 <br />z<sub>A</sub> proportional to n<sup>k</sup> with -1.5 < k < -1 | |||
* return current velocity<br />v<sub>R</sub> proportional to v<sub>S</sub> <br />v<sub>R</sub> proportional to n<sup>-1</sup> | |||
The diagram (Picture 1) shows the spectrum of possible calculated results given the boundary conditions at a [[cross-section]] of the Lower Elbe compared to the measurement data won from a hydraulic [[model]] of the BAW-DH. | |||
Not only is the interaction between ship and [[waterway]] critical for forming a prognosis on ship induced loading in waterways with varying non-uniform cross-sections, but also the physical processes of wave spreading such as refraction and [[shoaling]] are critical and must be accounted for in the calculations (without parameterization). | |||
Traditional empirical and analytical approaches only allow for an inadequate estimation of the ship induced loading caused by sea-going merchant shipping on large fairways with varying non-uniform cross-sectional geometries, especially in tidal regions. Thus these approaches are inadequate for calculating the magnitude of future loading on waterways. | |||
<br /> | |||
==Hydrodynamic Numerical Methods== | |||
[[de:Hydrodynamisch-numerische Methoden]] | |||
[[File: Seb.Bild4.jpg|thumb|Picture 1: Calculated water level change caused by a PANMAX container ship]] | |||
Through use of the presently available computer hardware and a new form of the BOUSSINESQ equation describing the spreading of shallow wind generated water waves (NWOGU, 1993)<ref>NWOGU, O., Alternative form of Boussinesq equation for nearshore wave propagation, J. of [[Waterway]], [[Port]], Coastel and [[Ocean]] Engineering, Vol. 119, No. 6, ASCE, USA, 1993</ref>, it was possible to simulate ship waves in laterally and depth limited waterways where the wave effects of refraction, [[shoaling]], diffraction, reflection and most recently also current refraction as well as squat and [[trim]] (albeit at subcritical speed to date) could be included. Extensive calculations using the WAKE2D numerical [[model]] of the National Research Council of Canada - Canadian Hydraulic Center ([http://www.nrc-cnrc.gc.ca/eng/ibp/chc.html NRC-CHC, 1997]) <ref>NRC-CHC, Numerical [[Model]] Study of Ship-Induced Waves und Currents in the Elbe [[Estuary]], Controlled Technical Report, HYD.CTR-093 (unpublished), Ottawa, Canada, 1997</ref>were commissioned by the BAW-DH as part of an investigation of the Lower Elbe river. The results of the WAKE2D calculations show that the amplitudes of the short period waves are estimated to be much higher than those measured in the physical [[model]]. | |||
Other theoretical [[Numerical Methods|numerical methods]] for modeling currents around ships such as FANKAN (Fluid-Automaten-Net for Canals for large blockage factor ships; PAGEL/FÜHRER, 1989)<ref>PAGEL, W. und FÜHRER, M., Umströmungs- und Widerstandsverhalten völliger Schiffe bei Kanalfahrt. Ergebnisse einer diskreten Modellierung und ihrer experimentellen Verifizierung, Mitteilungen der Forschungsanstalt für Schiffahrt, Wasser- und Grundbau, Schriftenreihe Heft 3, Berlin, 1989</ref>are not so far developed that they accurately discretize hydrodynamically optimized ship forms (e.g., a bulb-bow) and thus falsify the dynamic loading of sea waterways. | |||
Preliminary results using another [[model]] called SHALLOWTANK (CHEN, 1998)<ref>CHEN, X.-N., Schiffswellenbildung über einer querveränderlichen Topographie, Abstracts - 19. Duisburger Kolloquium Schiffstechnik/ Meerestechnik, Das Schiff für überkritische Fahrt, Duisburg, 1998</ref> (CHEN/ULICZKA, 1999)<ref>CHEN, X.-N. und ULICZKA, K., On Ships in Natural Waterways, Proceedings of Int. Conf. on Coastal Ships and Inland Waterways, The Royal Institution of Naval Architects, Feb. 1999, London 1999</ref> show qualitative, and to a certain degree, quantitative agreement with the measurements of ship runs acquired in the physical [[model]] of the BAW-DH. The SHALLOWTANK [[model]] has already been used for calculating ship induced loading for trans- and supercritical ship speeds (CHEN, 1997)<ref>CHEN, X.-N., Theoretische Grundlagen der Wellenwiderstandseliminierung bei überkritischer Fahrt, besonders durch den Einsatz gekrümmter Katamarane, Proceedings - 18. Duisburger Kolloquium Schiffstechnik/Meerestechnik, Das Schiff in begrenzten Gewässern, Duisburg, 1997</ref>. It is conceivable that this program could be applied for calculating ship induced loading of inhomogeneous waterways when the necessary verification calculations for a validation have been performed. | |||
The WAKE2D and SHALLOWTANK models are "state-of-research" but are still somewhat scientifically controversial tools for studying ship-sea [[waterway]] interaction. | |||
A reliable quantitative prognosis for ship induced loading of sea waterways can presently only be obtained using properly scaled physical models. | |||
== References == | |||
<references /> | |||
<br /> | |||
---- | ---- | ||
back to [[Hydraulic Modelling]] | back to [[Hydraulic Modelling]] | ||
Latest revision as of 09:12, 21 October 2022
The change in draught- and speed-related ship-induced loading on the shipping routes entails a definition of the characteristic parameters (e.g. ship wave system, displacement current) and requires knowledge of the functional relationships (e.g. ship speed and vessel width, shipping channel conditions, passing clearance). Picture 1 shows a diagram of the ship wave system among others.
Since the start of the new century, a large number of analytical and empirical methods have been developed for calculating the interaction of ship and waterway. Initial calculations with hydrodynamic-numerical models reveal deviations compared to the results of hydraulic scale models, so that these numerical models cannot yet be viewed as a confirmed scientific aid for determining upgrading-related changes to ship-induced loading in shipping channels. At the moment, it is only possible to make confirmed quantitative predictions of ship-induced loadings in inhomogeneous waterways by means of hydraulic model tests in a scientifically confirmed model scale (state-of-the-art engineering and science).
In recent years, the BAW Hamburg office has looked at the issue of the interaction between seagoing ship and tidal fairways both with studies on hydraulic models and with field study measurements.
Definition of the Characteristic Parameters
A moving ship generates waves of different periods as a consequence of its displacement current causing pressure and water level changes at its bow, stern and alongside its hull. The following parameters describe the ship wave and current system, for example, for a ship moving in an estuary at subcritical speed (ship speed less than the phase speed of the prevailing waves):
- the bow pressure (sB) directly at the hull,
- the water level depression (zA) at the side of the ship,
- the stern wave (HP) which is a part of the long period primary wave system,
- the secondary wave superimposed on the primary wave system (HS),
- velocity (vR) of the simultaneously occurring return current.
The water level changes for a depth- and width-limited waterway, as seen by an observer from the bank, are shown as a vertically exaggerated sideview in the above sketch.
Functional Relationships
The parameters for the water level and current variations caused by a moving ship are a function of:
- ship velocity vS and the passing distance L
- ship dimensions (length l, width b, draught t, submerged midship cross-section AS)
- total hydrodynamic resistance of the ship (ship form) in the canal RT,K
- waterway conditions (water level B and bed width BS, water depth d, cross-section and area A, bank profile and slope 1 : m)
- current conditions in the waterway
- other influences such as waterway bend, type of propulsion, water density.
The essential parameters for the ship induced loading for fairways have been shown to be:
- the ship velocity (vS)
- the passing distance (L) to the bank edge which defines the hydraulic partial cross-section (AT)
- the water depth to draught ratio (d/t), and the cross-section ratio AT / 0,5 AS.
To illustrate more simply the physical processes occurring when a ship is moving in a waterway of varying non-uniform cross-section, one may think of the waterway cross-section as being divided into two parts AT1 and AT2, through each of which half of the ship's displacement passes. Thus each bank experiences a qualitatively different ship induced loading as is determined by the partial cross-section ratios AT1 / 0,5 AS and AT2 / 0,5 AS.
Analytical and Empirical Methods
Traditional Methods
Whereas analytical derivations can be used for the calculation of the water level depression zA (e.g. KREY, 1913; CONSTANTINE, 1960; BOUWMEESTER et al., 1977; FÜHRBÖTER, 1982), the calculation methods for determining the wave heights of ship waves, often aided by model studies and/or field measurements, are empirical (e.g., RÖMISCH, 1969). Though the short period secondary waves are taken into account by some of the empirical approaches, they are not known in detail as functions of the described parameters. This is because these secondary waves are generated as a function of ship speed and ship form and as a result of the different pressure distributions along the body of the ship.
The following simplified relationships have been culled from the literature for the subcritical speed range (i.e., vS < 0.9·[g·d]0.5).This is the range used, for economical reasons, by merchant shipping:
- water level depression and wave height
zA proportional to vSk with 2 < k < 3.5
zA proportional to nk with -1.5 < k < -1 - return current velocity
vR proportional to vS
vR proportional to n-1
The diagram (Picture 1) shows the spectrum of possible calculated results given the boundary conditions at a cross-section of the Lower Elbe compared to the measurement data won from a hydraulic model of the BAW-DH.
Not only is the interaction between ship and waterway critical for forming a prognosis on ship induced loading in waterways with varying non-uniform cross-sections, but also the physical processes of wave spreading such as refraction and shoaling are critical and must be accounted for in the calculations (without parameterization).
Traditional empirical and analytical approaches only allow for an inadequate estimation of the ship induced loading caused by sea-going merchant shipping on large fairways with varying non-uniform cross-sectional geometries, especially in tidal regions. Thus these approaches are inadequate for calculating the magnitude of future loading on waterways.
Hydrodynamic Numerical Methods
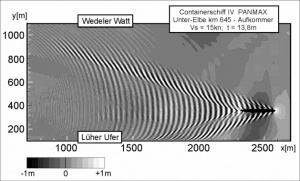
Through use of the presently available computer hardware and a new form of the BOUSSINESQ equation describing the spreading of shallow wind generated water waves (NWOGU, 1993)[1], it was possible to simulate ship waves in laterally and depth limited waterways where the wave effects of refraction, shoaling, diffraction, reflection and most recently also current refraction as well as squat and trim (albeit at subcritical speed to date) could be included. Extensive calculations using the WAKE2D numerical model of the National Research Council of Canada - Canadian Hydraulic Center (NRC-CHC, 1997) [2]were commissioned by the BAW-DH as part of an investigation of the Lower Elbe river. The results of the WAKE2D calculations show that the amplitudes of the short period waves are estimated to be much higher than those measured in the physical model.
Other theoretical numerical methods for modeling currents around ships such as FANKAN (Fluid-Automaten-Net for Canals for large blockage factor ships; PAGEL/FÜHRER, 1989)[3]are not so far developed that they accurately discretize hydrodynamically optimized ship forms (e.g., a bulb-bow) and thus falsify the dynamic loading of sea waterways.
Preliminary results using another model called SHALLOWTANK (CHEN, 1998)[4] (CHEN/ULICZKA, 1999)[5] show qualitative, and to a certain degree, quantitative agreement with the measurements of ship runs acquired in the physical model of the BAW-DH. The SHALLOWTANK model has already been used for calculating ship induced loading for trans- and supercritical ship speeds (CHEN, 1997)[6]. It is conceivable that this program could be applied for calculating ship induced loading of inhomogeneous waterways when the necessary verification calculations for a validation have been performed.
The WAKE2D and SHALLOWTANK models are "state-of-research" but are still somewhat scientifically controversial tools for studying ship-sea waterway interaction.
A reliable quantitative prognosis for ship induced loading of sea waterways can presently only be obtained using properly scaled physical models.
References
- ↑ NWOGU, O., Alternative form of Boussinesq equation for nearshore wave propagation, J. of Waterway, Port, Coastel and Ocean Engineering, Vol. 119, No. 6, ASCE, USA, 1993
- ↑ NRC-CHC, Numerical Model Study of Ship-Induced Waves und Currents in the Elbe Estuary, Controlled Technical Report, HYD.CTR-093 (unpublished), Ottawa, Canada, 1997
- ↑ PAGEL, W. und FÜHRER, M., Umströmungs- und Widerstandsverhalten völliger Schiffe bei Kanalfahrt. Ergebnisse einer diskreten Modellierung und ihrer experimentellen Verifizierung, Mitteilungen der Forschungsanstalt für Schiffahrt, Wasser- und Grundbau, Schriftenreihe Heft 3, Berlin, 1989
- ↑ CHEN, X.-N., Schiffswellenbildung über einer querveränderlichen Topographie, Abstracts - 19. Duisburger Kolloquium Schiffstechnik/ Meerestechnik, Das Schiff für überkritische Fahrt, Duisburg, 1998
- ↑ CHEN, X.-N. und ULICZKA, K., On Ships in Natural Waterways, Proceedings of Int. Conf. on Coastal Ships and Inland Waterways, The Royal Institution of Naval Architects, Feb. 1999, London 1999
- ↑ CHEN, X.-N., Theoretische Grundlagen der Wellenwiderstandseliminierung bei überkritischer Fahrt, besonders durch den Einsatz gekrümmter Katamarane, Proceedings - 18. Duisburger Kolloquium Schiffstechnik/Meerestechnik, Das Schiff in begrenzten Gewässern, Duisburg, 1997
back to Hydraulic Modelling
