Analytical methods – Groundwater flow: Difference between revisions
From BAWiki
No edit summary |
The LinkTitles extension automatically added links to existing pages (<a target="_blank" rel="nofollow noreferrer noopener" class="external free" href="https://github.com/bovender/LinkTitles">https://github.com/bovender/LinkTitles</a>). |
||
| Line 1: | Line 1: | ||
A wide range of analytical solutions are available for calculating groundwater flow. These generally consist of one-dimensional mathematical-physical models with highly simplified model assumptions. Even so, in many cases analytical solutions are capable of describing groundwater flow problems with adequate accuracy. Examples include steady state, vertical-plane inflow to a ditch and steady state rotationally symmetrical inflow to a well under varying boundary conditions both for confined and unconfined flow based on the Dupuit assumptions. Groundwater seepage at excavation pits can be calculated for simple geometric situations and boundary conditions by superposition of well flows based on the multi-well equation by Forchheimer. Solutions for transient flows are available both for inflow to pits and for well flow. The best known is Theis' well formula which is also used in the evaluation of pump tests. A compilation of analytical solutions for groundwater flow problems along with explanations of the basic assumptions and the mathematical derivations is provided e.g. by Odenwald et al. (2018). | A wide range of analytical solutions are available for calculating groundwater flow. These generally consist of one-dimensional mathematical-physical models with highly simplified [[model]] assumptions. Even so, in many cases analytical solutions are capable of describing groundwater flow problems with adequate accuracy. Examples include steady state, vertical-plane inflow to a ditch and steady state rotationally symmetrical inflow to a well under varying boundary conditions both for confined and unconfined flow based on the Dupuit assumptions. Groundwater seepage at excavation pits can be calculated for simple geometric situations and boundary conditions by superposition of well flows based on the multi-well equation by Forchheimer. Solutions for transient flows are available both for inflow to pits and for well flow. The best known is Theis' well formula which is also used in the evaluation of pump tests. A compilation of analytical solutions for groundwater flow problems along with explanations of the basic assumptions and the mathematical derivations is provided e.g. by Odenwald et al. (2018). | ||
<gallery> | <gallery> | ||
File:08_Grundwasserstroemung_01.jpg|Picture 1: Dam undercurrent in a semi-confined aquifer | File:08_Grundwasserstroemung_01.jpg|Picture 1: Dam undercurrent in a semi-confined aquifer | ||
Latest revision as of 10:19, 21 October 2022
A wide range of analytical solutions are available for calculating groundwater flow. These generally consist of one-dimensional mathematical-physical models with highly simplified model assumptions. Even so, in many cases analytical solutions are capable of describing groundwater flow problems with adequate accuracy. Examples include steady state, vertical-plane inflow to a ditch and steady state rotationally symmetrical inflow to a well under varying boundary conditions both for confined and unconfined flow based on the Dupuit assumptions. Groundwater seepage at excavation pits can be calculated for simple geometric situations and boundary conditions by superposition of well flows based on the multi-well equation by Forchheimer. Solutions for transient flows are available both for inflow to pits and for well flow. The best known is Theis' well formula which is also used in the evaluation of pump tests. A compilation of analytical solutions for groundwater flow problems along with explanations of the basic assumptions and the mathematical derivations is provided e.g. by Odenwald et al. (2018).
-
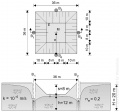
Picture 1: Dam undercurrent in a semi-confined aquifer
-
Picture 2: Multi-well system in an unconfined aquifer
-
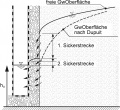
Picture 3: Well inflow in an unconfined aquifer
-
picture 4: Groundwater potential assuming a constant extraction rate from the well and confined groundwater flow
Literature
Odenwald, B.; Hekel, U.; Thormann, H.: Kap. 9: Grundwasserströmung – Grundwasserhaltung. In: Witt, K.J. (Hrsg.): Grundbau-Taschenbuch, 8. Auflage, Teil 2: Geotechnische Verfahren, S. 635 - 819, Ernst & Sohn, Berlin, 2018.
back to: Analytical methods