Groundwater models: Difference between revisions
From BAWiki
Created page with "200px|thumb|right|Picture 1: Groundwater model for retention area weir, Kehl File:08_Grundwasserstroemung_02.jpg|200px|thumb|right|Pi..." |
The LinkTitles extension automatically added links to existing pages (<a target="_blank" rel="nofollow noreferrer noopener" class="external free" href="https://github.com/bovender/LinkTitles">https://github.com/bovender/LinkTitles</a>). |
||
| (3 intermediate revisions by one other user not shown) | |||
| Line 1: | Line 1: | ||
[[File: | [[File:09_Grundwassermodelle_01.jpg|200px|thumb|right|Picture 1: Groundwater model for retention area weir, Kehl]] | ||
[[File: | [[File:09_Grundwassermodelle_02.jpg|200px|thumb|right|Picture 2: Transient dam saturation caused by a leak in the canal lining]]The basis for calculating groundwater and seepage flows is their description using mathematical models. Numerical computational methods based on the finite element method (FEM) or the finite difference method (FDM) offer a suitable range of instruments for dealing with complex geohydraulic issues. These computational models enable the spatial variability of the ground and external inflows as well as the change in the water saturation conditions to be taken into account. Computational groundwater flow models are used to investigate a wide range of issues, including: | ||
* to determine the impact of construction measures in waterways on the large-scale groundwater conditions, | * to determine the impact of construction measures in waterways on the large-scale groundwater conditions, | ||
* to search for alternatives for minimising unwanted impacts of construction measures on the existing groundwater system, | * to search for alternatives for minimising unwanted impacts of construction measures on the existing groundwater system, | ||
* to ascertain the forces resulting from groundwater flow on the ground and on the structure and | * to ascertain the forces resulting from groundwater flow on the ground and on the structure and | ||
* to compare suitable groundwater drainage or relief measures for reducing unwanted groundwater effects. | * to compare suitable groundwater [[drainage]] or relief measures for reducing unwanted groundwater effects. | ||
[[File: | [[File:06_Numerische_V_01.jpg|200px|thumb|right|Picture 3: Groundwater model for the excavation pit for Minden lock]]The use of numerical groundwater models can entail differing levels of spatial resolution (one-dimensional, two-dimensional along a horizontal or vertical plane, three-dimensional) and complexity (steady-state/transient, saturated/unsaturated), depending on the specific issue and on the available data. | ||
[[File: | [[File:09_Grundwassermodelle_03.jpg|200px|thumb|right|Picture 4: Groundwater model (quarter model) for a dam with culvert structure]]Vertical-plane calculations are suitable for groundwater flows that occur with elongated [[Building structure|building structures]] with largely unchanging hydraulic boundary conditions and presumably negligible flow normal to the computational plane (e.g. flow through a canal or river embankment). In the case of flows with a free [[groundwater surface]] where the part of the [[model]] domain which is saturated with water is not known in advance or changes during the time period observed, a saturated/unsaturated numerical flow calculation is carried out (e.g. to determine the impact of [[Flood|floods]] or rapid [[water level]] fluctuations on the flow through an embankment). In the unsaturated zone, the functional interrelationship between pore water pressure, degree of saturation and hydraulic conductivity must be taken into account. Given that these relationships of soil [[hydraulics]] are non-linear, the numerical calculation requires much more time and effort than in the case of completely water-saturated flows. | ||
3D numerical calculation of the groundwater flow is required if the geometric situation or the hydraulic boundary conditions result in a pronounced 3D flow field that cannot be represented adequately by simplified groundwater models. This is usually the case, for example, with groundwater modelling of flows around a building structure to determine the forces resulting from groundwater pressure and flow. Three-dimensional modelling, particularly when taking account of saturated/unsaturated flows, requires an in-depth knowledge of geohydraulics and the relevant numerical computational methods, together with extensive experience in modelling. | 3D numerical calculation of the groundwater flow is required if the geometric situation or the hydraulic boundary conditions result in a pronounced 3D flow field that cannot be represented adequately by simplified groundwater models. This is usually the case, for example, with groundwater modelling of flows around a [[building]] structure to determine the forces resulting from groundwater pressure and flow. Three-dimensional modelling, particularly when taking account of saturated/unsaturated flows, requires an in-depth knowledge of geohydraulics and the relevant numerical computational methods, together with extensive experience in modelling. | ||
---- | ---- | ||
Latest revision as of 10:22, 21 October 2022
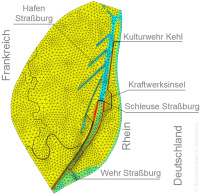
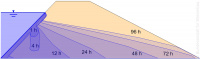
The basis for calculating groundwater and seepage flows is their description using mathematical models. Numerical computational methods based on the finite element method (FEM) or the finite difference method (FDM) offer a suitable range of instruments for dealing with complex geohydraulic issues. These computational models enable the spatial variability of the ground and external inflows as well as the change in the water saturation conditions to be taken into account. Computational groundwater flow models are used to investigate a wide range of issues, including:
- to determine the impact of construction measures in waterways on the large-scale groundwater conditions,
- to search for alternatives for minimising unwanted impacts of construction measures on the existing groundwater system,
- to ascertain the forces resulting from groundwater flow on the ground and on the structure and
- to compare suitable groundwater drainage or relief measures for reducing unwanted groundwater effects.
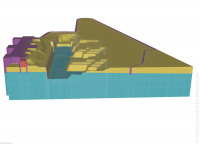
The use of numerical groundwater models can entail differing levels of spatial resolution (one-dimensional, two-dimensional along a horizontal or vertical plane, three-dimensional) and complexity (steady-state/transient, saturated/unsaturated), depending on the specific issue and on the available data.

Vertical-plane calculations are suitable for groundwater flows that occur with elongated building structures with largely unchanging hydraulic boundary conditions and presumably negligible flow normal to the computational plane (e.g. flow through a canal or river embankment). In the case of flows with a free groundwater surface where the part of the model domain which is saturated with water is not known in advance or changes during the time period observed, a saturated/unsaturated numerical flow calculation is carried out (e.g. to determine the impact of floods or rapid water level fluctuations on the flow through an embankment). In the unsaturated zone, the functional interrelationship between pore water pressure, degree of saturation and hydraulic conductivity must be taken into account. Given that these relationships of soil hydraulics are non-linear, the numerical calculation requires much more time and effort than in the case of completely water-saturated flows.
3D numerical calculation of the groundwater flow is required if the geometric situation or the hydraulic boundary conditions result in a pronounced 3D flow field that cannot be represented adequately by simplified groundwater models. This is usually the case, for example, with groundwater modelling of flows around a building structure to determine the forces resulting from groundwater pressure and flow. Three-dimensional modelling, particularly when taking account of saturated/unsaturated flows, requires an in-depth knowledge of geohydraulics and the relevant numerical computational methods, together with extensive experience in modelling.
back to: Numerical Methods
