Program "PeTra"
From BAWiki
PeTra Programme Fairway routing in streams as function of water level
When preparing a development plan for fairways or the execution of a navigability analysis in streams, the water and shipping administration would pass development guidelines for each body of waters. These development guidelines are mainly based on the guidelines for standard cross-sections of navigation canals (see procedure “TRASSE”). In detail, this means that the Graewe formula is applied for calculating the necessary swept area for inland vessels. However, for passage in running waters, new standards are being applied to the drift angles that should be used; these have mostly been determined by in-situ studies of ship movement dynamics in the respective body of water. A disadvantage of this procedure is the fact that the results of the in-situ measurements only apply to the studied discharge situation. This procedure does not consider differences in the flow velocity dependent on different sections. Furthermore, when drawing up development guidelines, measurements can only be undertaken once the wanted discharge conditions have appeared.
In order to avoid these disadvantages and to minimize expensive in-situ measurements, a method has been developed on the basis of the TRASSE procedure for the computational estimation of the impact of flow velocity on the necessary traffic area of inland vessels.
Purpose of the software
As the principle of one-by-one positioning has proved itself for planning fairways in non-running waters, we attempted to apply it to running waters too. For this technique it is crucial to know the position of the pivot point (tactical turning point) at the vessel. In-situ measurements showed that, analogous to non-running waters, the pivot point position does not depend on the curve radius but changes according to flow velocity, travelling speed and travel direction. This resulted in the following objectives for the software to be developed:
- The impact of the waters’ flow velocity as well as the vessel’s travelling speed and travel direction on the traffic area needs of the inland vessels has to be considered.
- The procedure should be applicable to all types of inland vessels.
- Curve radii ranging from straight ahead travelling down to one vessel length should be considered.
- It should be possible to integrate the alignment results into MicroStation, the CAD system of the German Federal Waterways and Shipping Administration (WSV).
Theoretical basis of the procedure
When developing a calculation method meeting the above requirements two fundamental problems had to be solved: The first problem of modelling the impact of flow velocity has already been mentioned and will be treated later. The second problem consists in setting a course axis (the fact that it is necessary for such a course axis to exist has already been explained in the TRASSE procedure) which reflects a skipper’s way of thinking. For a non-running body of water it can be constructed directly, since the progression of the course axis only depends on a few nautical conditions (tangential transition from straight line–circle–straight line, minimum radius > vessel length). In running water with a sufficiently wide fairway (e.g. River Rhine) the skipper takes local conditions into account when choosing the course. As the fairway is located in a natural streambed it has neither a flat bottom nor a standard profile. The course taken by an experienced skipper would largely depend on the distributions of water depth and flow velocity in the riverbed. It is also affected by the size and draught of a vessel. A fully laden dangerous goods tanker would rather be guided by water depths and a container vessel with a smaller draught by flow velocities; this means that despite identical dimensions, the two vessels would take different courses. If ship dimensions change, the necessary traffic area for the vessel will change too, and with identical discharge conditions far different optimum ship paths may result.
Theoretical basis for generating course axes for inland vessels in free flowing waters
When developing the method of generating course axes automatically we tried to reflect a skipper’s way of thinking. As input data for creating a course axis, information is required on:
the vessel:
- dimensions, e.g. length and width
- draught
- characteristics concerning the dynamics of ship movement (estimated position of pivot point) etc.
the parameters of the body of water having an impact on the course axis:
- depth distribution over the cross-section
- distribution of flow velocities over the cross-section
- water level etc.
In order to enable a uniform evaluation of the different parameters, the concept of “navigability potential” has been introduced where all above parameters can be converted into one potential. For this conversion, all fairway parameters throughout the cross-section must be known as lateral section (“strips”) information (e.g. velocity strips averaged over the depth with a finite width etc.). Standardising the parameter values of the individual strips to potentials on a scale ranging from 0 to 100 makes it possible to evaluate navigability of the different profile sections with regard to this parameter. At the same time it allows comparison and superposition of the potential trends of different parameters so that in the end an overall evaluation of the navigability of each profile cross-section is possible.
Potentials are converted in the following way: If a high parameter value is considered to be optimum, the maximum in the profile corresponds to a potential of 100. Otherwise the smallest potential 1 is assigned to the highest parameter value (e.g. flow velocity: the vessel moving upstream looks for slow running water – highest velocity becomes potential 1 – and the vessel moving downstream looks for fast running water – maximum velocity becomes potential 100). The potential minimum 0 is only used when a profile section is to be considered as non-navigable once the parameter limit has been exceeded. This applies to the parameters of water depth, fairway limit and right-hand traffic; the idea is to assess, if needed, the profile strips outside the fairway as principally non-navigable or to force the observation of right-hand traffic.
Potential Pi of a single parameter in the i-th profile strip is obtained as follows:
If the maximum value of a parameter is considered to be optimal:
[math]\displaystyle{ P_i = P_{min} + \left[(P_{max} - P_{min}) * \frac{W_i - W_{min}}{ W_{max}-W_{min}}\right] }[/math]
If a small parameter value is aimed at, the following applies:
[math]\displaystyle{ P_i = P_{min} + \left[(P_{max} - P_{min}) * \frac{W_{max} - W_i}{ W_{max}-W_{min}}\right] }[/math]
| Pi | Potential in the i-th profile zone BAW |
| Pmin | Lowest potential (always Pmin=1) |
| Pmax | Highest potential (always 100) |
| Wi | Parameter value in the i-th profile strip |
| Wmin | Smallest parameter value on whole profile average |
| Wmax | Highest parameter value on whole profile average |
When evaluating water depth, the value is derived from the following difference:
[math]\displaystyle{ W_i = T_{DIFFi} = T_{Wi} - (T_T + T_S + T_F) }[/math]
| TDIFFi | Depth difference in the i-th profile zone |
| TWi | Water depth in the i-th profile zone (from parameter file) |
| TT | Draught of vessel |
| TS | Squat of vessel |
| TF | Underkeel-clearance |
Analogous to this, the largest and smallest depth differences are determined on the profile section and Wmin and Wmax are used in Equation (1). If the depth difference assumes a value below 0, the profile section is not navigable and the potential is set 0. Otherwise it ranges between 1 and 100.
For an overall evaluation of the navigability taking into consideration all available waters parameters, areas of the same size (width b) are taken along each profile intersection line k; they are created with an increment s from the beginning of the first potential strip available up to the end of the last potential strip (Figure 2). Half a vessel width (B/2) is used as increment s. Width b of the profile zone corresponds to the minimum necessary “gate” width (“gate” being the area of the cross section chosen according to the potential where the ship is able and meaningful to pass through) and depends on the vessel dimensions (B, L) and its Cf value (relative position of the pivot point on the ship) as well as on the course axis radius. As the course axis does not yet exist, the radius of the fairway Rf in the profile km is used instead.
[math]\displaystyle{ b = B \;\;\; }[/math] on a straight line
otherwise in curves
[math]\displaystyle{ b = \sqrt{ (|R_f|+ B )^2 + (Cf*L)^2} - R_f \;\;\; }[/math] if 0.5 <=Cf < 1.0 or
[math]\displaystyle{ b = \left(\sqrt{ (|R_f|+ B )^2 + (Cf*L)^2} -R_f\right) - \left(\sqrt{(R_f^2 + ((Cf-1)*L))^2} - R_f\right) \;\;\; }[/math] if 1.0 <=Cf < 1.5
The potential mean value Pi in the zone b is determined for each of the n waters parameters. Here we take into account the fact that the width si of the potential strips can be variable as well as the fact that strips and profile sections can overlap. The sum of the n mean values Pi taking into consideration the weighting wi of each waters parameter then results in the potential sum PbSUM used for evaluation for each of the k profile sections.
[math]\displaystyle{ P_{bSUM} = P_1 * w_1 + P_2 * w_2 + ... + P_n * w_n }[/math]
In addition the program user can assign weightings to each parameter in order to control the influence of each parameter on the result. The profile section with the highest potential sum is considered to have optimal navigability and is referred to below as the “passage gate” or “gate”, the course axis should pass through. If on one or several profiles there are zones of a comparably high potential sum (the user can define the tolerance range), several equivalent gates and therefore numerous possible course axes arise on these profile sections; the programme would detect the one with the shortest route from these.
In addition to the above conditions it is possible to take the traffic situation into account when calculating the course axes. In this case the data of several vessels are defined. Furthermore, the programme must be able to determine the positions of all traffic participants (km along the course of the body of waters) in a given calculation cycle. A locus curve per vessel containing its km position at discrete points in time is used as database. Each vessel’s impact on other crafts is described by a “potential sink” around the ship body which can be parameterised; this potential sink may have an impact on the position of the other vessels’ passage gates on the profile sections and thereby on their course axis. Once the traffic-dependent course axis calculation has been completed, the movement of all vessels involved can be presented at the exact point of time with an execution speed that can be preset (Figure 3). Once the model course axes have been created, these routes are used to visualise the traffic.
Now that it is possible to calculate the course axes, modelling the dynamics of ship movement becomes necessary – for the purpose of determining the pivot point position as a function of local conditions.
Theoretical basis for modelling the dynamics of an inland vessel’s movement in free-flowing water
When travelling in non-running water, a vessel’s swept area only depend on its dimensions, the curve radii to be taken and, related to this, the associated drift angle. This is because a vessel assumes a drift when moving in a curve, whereby the ship body is subject to an oblique approach flow. This oblique approach flow results in hydraulic crosswise forces which compensate the centrifugal forces as a consequence of moving on a curved line. The travelling speed on land which has an impact on the magnitude of the centrifugal forces is equal to the travelling speed on water which determines the magnitude of the hydraulic crosswise forces. For vessels moving in running water, the travelling speeds on land and on water are different depending on upstream or downstream travel. When moving upstream, the travelling speed on water is higher than on land. When the approach velocity increases, the hydraulic crosswise forces also increase, thereby reducing the drift and the swept area. When moving downstream, however, the speed on water decreases. This means that hydraulic crosswise forces decrease and as a consequence the drift angle when travelling in a curve needs to be increased and the traffic area needs rise.
Formulating a mathematical-physical approach
The hydronumerical model is first developed for driving along a circular route under static conditions. By this simplification the problem concerning ship movement dynamics can be explained by the following physical facts: A mass is moving on a circular line. Circular motion causes centrifugal forces. Centrifugal forces need to be compensated by external forces so that the mass can stay on the circular line. While the vessel is moving, these external forces are generated by the skipper who, by well-directed rudder manoeuvres, makes sure that a drift angle arises. As a consequence of the drift the ship body is subject to an oblique approach flow and hydraulic crosswise forces are generated counterbalanced by the centrifugal forces.
Calculation of the centrifugal forces
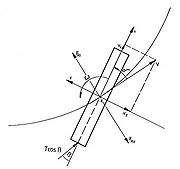
The derivation of the motion equation for determining the centrifugal forces is based on Kirchhoff’s equations of motion for a rigid body /1/. The equations of motion refer to a ship's fixed system of coordinates whose x-axis is on the centre line plane. The positive y-axis points out into the inner curve. The point of origin is located in the middle of the ship (Figure 4).
Following /2/ Kirchhoff’s equations of motion were further developed in such a way that force equations arise into the x and y direction. These read as follows:
[math]\displaystyle{ Fx(t) = (m + mx) \frac{d}{dt}Vx g(t) - (m + my) Vy g(t) \omega }[/math]
[math]\displaystyle{ Fx(t) = (m + my) \frac{d}{dt}Vy g(t) + (m + mx) Vx g(t) \omega }[/math]
In these equations of motion, Fx and Fy are the force components in the respective directions of the ship’s fixed system of coordinates. Ship velocity tangential to the path of motion was also resolved into these components. It corresponds to ship velocity over ground as this is responsible for the inertia. Furthermore, m is the vessel mass and ω the angular velocity of the rotation around the vertical axis. As vessels move in water, their own motion sets a water mass in motion. Therefore, contrary to a motion under vacuum, the ship mass while moving in water needs to be increased by the hydrodynamic masses (mx and my).
The force components of the x and y directions are converted into the tangential and radial fractions referred to the path. Only the radial force share should be considered for the model to be drawn up.
[math]\displaystyle{ Fra(t) = -Fx \sin(\delta(t)) - Fy \cos(\delta(t)) }[/math]
Assuming that the speed and drift angle do not change while moving in a curve, their derivations become 0 with respect to time. If we additionally introduce the non-dimensional path curvature Ω, the differential equation can be simplified as follows:
[math]\displaystyle{ Fra(t) = -\Omega \frac{Vg(t)^2}{L} [m+\sin(\delta(t))^2) my + \cos(\delta(t))^2 mx] }[/math]
where:
[math]\displaystyle{ \Omega = \frac{\omega}{Vg(t)} L }[/math]
L is the ship length.
Calculating hydraulic forces caused by oblique approach flow
During controlled motion the skipper generates a crosswise force at the stern of the vessel by well-directed rudder manoeuvres. This force causes a rotation of the ship body. Due to the superposition of progressing velocity and rotation, an oblique approach flow onto the ship body is produced. This oblique approach flow generates a crosswise force which, if equilibrium conditions are maintained, results in the ship moving on a circular path.
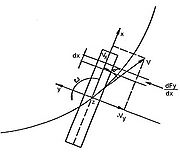
A momentum analysis on the ship body is carried out to calculate the hydraulic crosswise forces /3/. In doing so the approach velocity tangential to the moving direction is resolved into its components along and at right angles to the vessel’s longitudinal axis. In addition we presume that the water mass impacting the ship body crosswise is diverted by the ship body. As a consequence of the periodic change of the liquid’s impulse within a control plane with the differential width dx (Figure 5), a local crosswise force is generated at the ship body.
The y component of the hydrodynamic momentum in the control plane caused by the ship velocity relative to the water Vw is:
[math]\displaystyle{ dI_{Fl}=\tilde{m}y(x) \, Vw(t) \, \sin(\delta(x)) dx }[/math]
The drift angle δ(x) dependent on the position along the ship axis is converted into a time-dependent drift angle by a superposition of progress velocity V(t)•sin(δ(t)) and the crosswise approach flow resulting from rotation around the z-axis -ω•x. From this follows:
[math]\displaystyle{ \sin(\delta(x)) = \sin(\delta(t)) - \frac{x}{R} }[/math]
Calculating the hydrodynamic mass
If a body is accelerated under vacuum, a force must act on it to overcome its inertia. If the body is moving in water in addition, particles of the liquid need to be accelerated in order to avoid the body and refill the space which has become free in the meantime at the body‘s former position. Kinetic energy is therefore applied to the body of water as a consequence of acceleration. Entering this into the initial relation, the following applies to the kinetic energy fed to the fluid following a body’s accelerated motion:
[math]\displaystyle{ E_{Fl}=-\frac{\rho}{2} \int_A \Phi \frac{\partial \Phi}{\partial n} dA }[/math]
With the velocity potential known, the kinetic energy
[math]\displaystyle{ E = \frac{m}{2} \nu^2 }[/math]
fed to the fluid can be calculated by this relation. By analogy with a mass moving under vacuum, kinetic energy can be calculated using the well-known formula. Finally, by using this definition it becomes possible to express kinetic energy as a mass, i.e. the so called hydrodynamic mass, which in motion equations is added to the vessel mass. The hydrodynamic mass m̃y(x) (per unit length) can be calculated using the inertia coefficient according to Lewis /4/.
[math]\displaystyle{ m_h = -\frac{\rho}{\nu^2} \int_A \Phi \frac{\partial \Phi}{\partial n} dA }[/math]
The following then applies:
[math]\displaystyle{ \tilde{m}y(x) = \frac{\rho}{2} \pi c(x) T(x)^2 }[/math]
Here c(x) is the Lewis coefficient at the point x of the ship body corresponding to the frame form there and T(x) is the local draught. The Lewis coefficient for the frame forms most frequent in inland navigation can be calculated using a potential theory approach. During circular driving under static conditions, periodic change of the impulse within a controlled section generates the local crosswise force.
[math]\displaystyle{ dFy(x) = d \left[ \frac{\rho}{2} \pi c(x) T(x)^2 Vw(t) \left(\sin(\delta(t)) - \frac{x}{R} \right) \right] \frac{dx}{dt} }[/math]
Here dx/dt is the speed on water provoking the crosswise forces. This approach is only applicable to small drift angles. With larger angles, eddies are generated around the stern; and the flow around the ship body deviates more and more from the assumption of parallel flow around the frames. Therefore, according to /5/ an additional share needs to be taken into consideration.
[math]\displaystyle{ sgn(\delta(t)) \, Cws \frac{\rho}{2} [Vw(t) \sin(\delta(t))]^2 \int^{\frac{L}{2}}_{\frac{_L}{2}} T(x) dx }[/math]
By means of integration over the ship length and introducing non-dimensional line curvature Ω, the hydraulic crosswise force can be calculated using the following equation:
[math]\displaystyle{ Fy(t) = \left[I1 \cos(\delta(t)) \sin(\delta(t)) - I2 \cos(\delta(t)) \frac{\Omega}{L} - I3 \frac{\Omega}{L} \cos(\delta(t)) + \frac{Cws}{\pi} I4 \right] \frac{\rho}{2}\pi Vw(t)^2 }[/math]
In this equation I1 to I4 represent the following integrals:
[math]\displaystyle{ I1 = \int^{\frac{L}{2}}_0 \left(\frac{d}{dx}c(x)T(x)^2 \right) dx }[/math]
[math]\displaystyle{ I2 = \int^{\frac{L}{2}}_0 \left(\frac{d}{dx}c(x)T(x)^2 \right) xdx }[/math]
[math]\displaystyle{ I3 = \int^{\frac{L}{2}}_{\frac{_L}{2}} \left(c(x)T(x)^2 \right) dx }[/math]
[math]\displaystyle{ I4 = \int^{\frac{L}{2}}_{\frac{_L}{2}} T(x) \left( \sin(\delta(t)) - \frac{\Omega x}{L}\right)^2 dx }[/math]
For integrals I1 and I2 integration is only carried out over L/2 as the impulse deviation resulting from changing cross-section components is disturbed by detachment around the stern.
Calculating the pivot point position
While moving on the stationary turning circle, centrifugal forces and the radial share of crosswise forces are in equilibrium due to the oblique approach flow, i.e.:
[math]\displaystyle{ 0 = Fra(t) \, Fy(t) \cos(\delta(t)) }[/math]
The hydrodynamic masses contained in the expression for centrifugal forces can also be calculated using the Lewis’ coefficients. Here the impact of the three dimensional flow around the vessel is taken into account by correction factors according to Munk (R1 and R2). This gives the following results for mx and my of a double-body mirrored at the water level plane:
[math]\displaystyle{ myd = R2 \, \rho \, \pi \int^{\frac{L}{2}}_{\frac{-L}{2}} c(x) T(x)^2 dx }[/math]
[math]\displaystyle{ mxd = R1 \, \rho \, \pi \int^{\frac{L}{2}}_{\frac{-L}{2}} c(x) T(x)^2 dx }[/math]
The integrals contained in these equations have already been formulated as I3. As these studies only apply to travel on the stationary turning cycle, time-dependence does not need to be considered. Furthermore the following results from the circular motion’s kinematics:
[math]\displaystyle{ \Omega=\frac{L}{R} }[/math]
So, after solution of the equation you receive the functional relationship between the line radius R and the drift angle δ:
[math]\displaystyle{ R(\delta) = \frac{2Vg^2[m+\rho \,\pi \, I3 (\sin(\delta)^2 R2 + \cos(\delta)^2 R1) ]+Vw^2 \, \rho \, \pi \, \cos(\delta)^2 (I2 + I3)} {[\cos(\delta) \sin(\delta) \, \pi \, I1 + Cws \, I4] \rho \cos(\delta) Vw^2} }[/math]
In this function the following dependencies have been taken into consideration:
- The impact of flow speed when going upstream as well as downstream is achieved by differentiating between speed on ground (Vg) and speed on water (Vw).
- Coefficient Cws considers the forces caused by the occurrence of separation at the stern while progressing with large drift angles. Only a few experimental values exist in the literature regarding its magnitude for seagoing vessels. For inland navigation purposes its extent needs to be determined by in-situ studies.
- Integrals I1 to I4 mainly consist of the course of the quantity c(x)T(x) along the ship body. Here T(x) is the local draught at the point x and c(x) the appropriate Lewis coefficient. So the main ship dimensions (length L and draught T) are included in the function via the integral over the ship length. The width impact is considered indirectly via the inertia coefficients according to Lewis. These also comprise the local hull form of the vessel and exist for frequent hull forms or can be calculated using conformal mapping. Subsequent to the integration, the ship body’s form is therefore introduced into the calculation as an influencing parameter via the form integrals.
Finally we would like to point out that studies have been undertaken in the past to determine the influence of shallow water on the magnitude of the Lewis coefficients. Experience is therefore available on how to consider the impact of shallow water effects on the magnitude of the developing drift angle in a mathematical model.
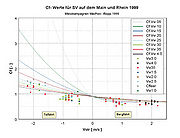
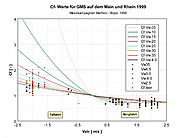
As already shown, the magnitude used in the trial calculation for the wake coefficient Cws is a mean value taken from sea navigation. For inland vessels, no experiences exist in the literature that could be used. So, for dimensioning purposes, Cws values have been derived from statistically reliable findings about the pivot point position while progressing on canals, and these have been transposed to running waters. This is possible because the Cws value mainly depends on the form of the after-body. Applying these wake values we modelled a large motor vessel and calculated the Cf value’s dependences on the body of waters’ flow velocities and the vessel’s travelling speed on water as shown in Figure 6.
In the diagram, the river’s flow velocity Vstr is entered as abscissa. The vessel’s upstream travel is marked with a positive sign, its downstream travel with a negative sign. The Cf value is entered as ordinate as a non-dimensional quantity. A value of 0 means that the pivot point is located in the vessel stern. With the value being 1, it is located in the vessel’s bow. With values larger than 1, the pivot point is located in front of the vessel. According to the preliminary theoretical considerations, the Cf value depends on the body of water‘s flow velocity and on the vessel’s travelling speed on water. Therefore a separate function was calculated for each travelling speed studied, and their graphs marked in different colours. The assignment between colour and vessel speed on water is given in the diagram’s legend.
Summarising, the preliminary considerations provide the following results:
- The pivot point’s position is independent of the driven curve radius R for R>L.
- The water’s flow velocity has an impact on the pivot point position and therefore on the vessel’s swept area width. When going upstream its position moves towards the vessel centre, resulting in a slight decrease in swept area width. When moving downstream this point moves towards or even in front of the bow, hereby enlarging the swept area width.
- The vessel’s travelling speed on water changes the magnitude of the flow speed impact on the pivot point position. Increasing the travelling speed causes a slight enlargement of swept area width when moving upstream and a decreasing swept area width when moving downstream.
Examples of use
PeTra Programme has been in actual use at the German Federal Waterways Engineering and Research Institute (Bundesanstalt für Wasserbau, BAW) since 1998. The component for Automatic Course Axis Generation is being developed further in parallel. The initial purpose of this function had been to generate an initial line at the beginning of the works on the basis of which development planning could be continued. When this mathematical model was first tested, it was established that the quality of the axes was higher than expected. For this reason the procedure was developed further with the aim that, by only changing the hydraulic conditions, realistic course axes can be generated such that navigability and bottleneck analyses can be undertaken for entire water level ranges within a short time.
Reference projects
| Project | Executing authority |
|---|---|
| Alignment project verification for developing the River Weser middle section | BAW |
| Navigability analysis of River Saar | WSA (Wasser- und Schifffahrtsamt /local Office of the Federal Waterways and Shipping Administration) Eberswalde |
| Appraising the City of Magdeburg section regarding ship movement dynamics | WNA (Wasserstraßen-Neubauamt/ Waterways Construction Office) Berlin / BAW |
| Appraising Kitzingen bridge over the River Main regarding ship movement dynamics | BAW |
| Bottleneck analysis of the River Rhine | BAW |