Influence of Ship Length and UKC on the Squat and Trim of very large Containerships
From BAWiki
Author: K. Uliczka
Boundary Conditions
Investigations of the influence of ship length on the behavior of very large POST-PANMAX container ships (PPM) were carried out in the shallow water tank of the BAW-DH (length: approx. 100 m, width: approx. 33 m, maximum depth: 0.7 m) with a model scale of 1 : 50. By adding mid-ship sections to an available PPM container ship model, very long PPM container ships with lengths of 400 and 450 m (instead of 350 m), beams of 50 m, and drafts of 17 m could be simulated. The depth-FROUDE numbers were 0.28 < Frh < 0.67. The resulting REYNOLDS numbers were 3.8 · 106 < Re < 9.9 · 106 (factor 10 > ReCRIT,erf).
The investigation's prognosis capability was guaranteed by adhering to the geometric and dynamical conditions dictated by dimensional analysis.
The corresponding block coefficients cB = 0.677 - 0.837 - 0.961, for ships with extended lengths, falsely produce a (arithmetically high) coefficient of fineness which does not reflect the actual high slenderness ratio of the model ships (SG = 6.0 - 6.1 - 6.3).
Squat and trim were recorded in the measurement crossection using the point-wise laser-geometric method according to ERYUZLU et al. (1994). Depending upon ship speed, an accuracy of the prognostized values at bow and stern of DS < 1 mm (Model) was obtained.
Results
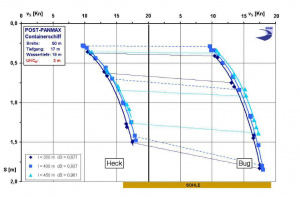
The influence of ship length may be inferred from Graph 1:
- A general trend towards a decrease in squat for longer ships is to be expected, which becomes especially apparent for the comparison of the PPM350 with the PPM450 at higher ship speeds (difference DS approx. 0.3 m at a ship speed of vS = 17 Kn).
- Above a ship speed of about vS = 15 Kn (Frh ca. 0.6) all ships show a higher than proportional increase in squat values.
- The PPM container ships show a lower speed dependent forward trim with increasing ship length.
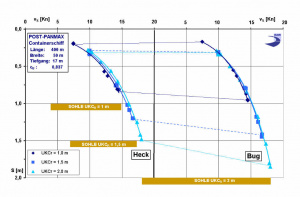
The influence of the under keel clearance (UKCR = under keel clearance for static conditions) is shown in Graph 2:
- For a constant displacement (t = constant), the influence is primarily seen in the stern squat: for a given ship speed, greater keel clearance = less squat.
- For the keel clearances investigated UKCR = 1.0 - 1.5 - 2.0 m (h/t = 1.06 - 1.09 - 1.12)), the orientation of the ship first changes steadily to a forward trim at higher speeds. Even for an aft trim (specified for static conditions), a forward trim is established at higher ship speeds (approx. FRh > 0.6; UKCR= 2.0 m).
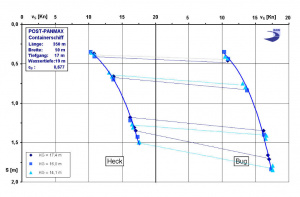
The distance of the the center of gravity above the keel (KG) only minimally influences the behavior of the ship (Graph 3):
- Only a minimal dependence of the squat on the KG (DKG up to approx. 3 m) could be measured in the investigation with the PPM 350.
- An increase in the distance of the center of gravity above the keel causes a "softer" ship behavior in waves. There is no definite influence of the size of the KG on the trim angle in calm water.
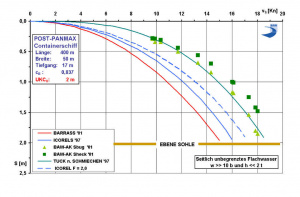
A prognosis for the squat and trim behavior of large PPM container shipsis not possible on the basis of "classic" analytical and empirical approaches, as has been shown in a comparison of calculations and measurements in a hydraulic model (e.g., squat in Graph 4):
- The large differences in the squat of very large PPM container ships between the squat derived from the formulas used by the WSV (ICORELS and BARRASS respectively) and the results from the hydraulic model, underlines the necessity of such model investigations for coastal specific questions.
- Analytical approaches based on natural measurements for the Lower Elbe River (Graph 4, e.g., TUCK cited in SCHMIECHEN, 1997) as well as the approach of Tuck (1967), only show near-agreement with the presented model results for specific boundary conditions.
- A speed dependent reversal of the trim (e.g., from aft to forward) is not implemented in these analytical approaches.
For the present, the hydraulic model method is deemed to be state of the art. It is expected that, in the medium term (approx. 3 - 5 years), civil authorities will be using numerical methods for investigating these questions.
Recommendations
The following method is recommended for establishing navigation channel depths for laterally unbounded shallow water:
- Application of the approximate TUCK-Formula (SCHMIECHEN,1997) for estimating the squat when calculating the navigation channel depth.
- Procedure for calculating the navigation channel depth:
- Exact determination of the maximum squat value based on model investigations (for the present, hydraulic models).
- Establish a partial safety factor only after the exact maximum squat is known.
back to Ship Dynamics