Analytische Verfahren - Grundwasserströmung
Aus BAWiki
Für die Berechnung von Grundwasserströmungen existieren umfangreiche analytische Lösungen. Diese basieren i. A. auf eindimensionalen, mathematisch-physikalischen Modellansätzen mit stark vereinfachten Modellannahmen. Trotzdem können Grundwasserströmungsprobleme in vielen Fällen mit ausreichender Genauigkeit durch analytische Lösungen beschrieben werden. Beispiele dafür sind die stationäre, ebene Zuströmung zu einem Graben sowie für die stationäre rotationssymmetrische Brunnenzuströmung bei unterschiedlichen Randbedingungen sowohl für gespannte Strömungsverhältnisse als auch für ungespannte Strömungen unter Verwendung der Dupuit-Annahmen. Grundwasserhaltungen für Baugruben lassen sich bei einfachen geometrischen Verhältnissen und Randbedingungen durch Überlagerung von Brunnenströmungen auf Grundlage der Mehrbrunnenformel von Forchheimer berechnen. Lösungen für instationäre Strömungen existieren sowohl für die Grabenströmung als auch für die Brunnenströmung (Bild 1). Die bekannteste ist die Brunnenformel von Theis, auf deren Grundlage auch die Auswertung von Pumpversuchen erfolgt. Eine Zusammenstellung analytischer Lösungen für Grundwasserströmungsprobleme mit Erläuterung der grundlegenden Annahmen sowie der mathematischen Herleitungen wird z. B. von Odenwald et al. (2018) gegeben.
-
Bild 1: Unterströmung eines Deiches in einem halbgespannten Grundwasserleite
-
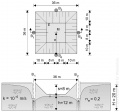
Bild 2: Mehrbrunnenanlage im ungespannten Grundwasserleiter
-
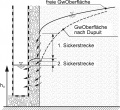
Bild 3: Brunnenzuströmung im ungespannten Grundwasserleiter
-
Bild 4: Grundwasserpotential bei konstanter Brunnenentnahme und gespannter Grundwasserströmung
Literatur
Odenwald, B.; Hekel, U.; Thormann, H.: Kap. 9: Grundwasserströmung – Grundwasserhaltung. In: Witt, K.J. (Hrsg.): Grundbau-Taschenbuch, 8. Auflage, Teil 2: Geotechnische Verfahren, S. 635 - 819, Ernst & Sohn, Berlin, 2018.
zurück zu: Analytische Verfahren