Wechselwirkung Boden-Bauwerk

Bild 1: 3D-Modell Baugrube Schleuse Sülfeld (MLK)

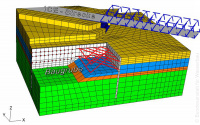
Zur Durchführung von Verformungs- und Standsicherheitsberechnungen an Bauwerken des Verkehrswasserbaus wird in zunehmendem Maße die Finite Elemente Methode (FEM) und in den letzten Jahren auch die Distinkte Elemente Methode (DEM) verwendet. Die FEM hat den Vorteil, dass komplexe Geometrien und Baugrundverhältnisse abgebildet werden können und außerdem die Interaktion zwischen Bauwerk und Baugrund erfasst werden kann.

Bild 2: Verformtes 2D-Modell der Schleuse Minden (Weser)

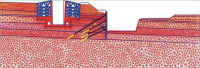
Durch die zunehmende Komplexität der Baumaßnahmen wie z. B. im Zuge des Neubaus von Bauwerken neben bestehenden Schleusen bei laufendem Schifffahrtsbetrieb oder bei der Nachrechnung des Trag- und Verformungsverhaltens bestehender Bauwerke spielen die genannten Vorteile des Verfahrens eine wichtige Rolle.

Bild 3: Spannungs-Setzungs-Kurven aus Ödometerversuch und Nachrechnung mittels FEM

Bild 4: Simulation von Wasserbausteinen mit der DEM

Je nach Erfordernis werden zwei - oder dreidimensionale Modelle zur Lösung des geotechnischen Problems erstellt. Zur Beschreibung des mechanischen Verhaltens des Bodens stehen dabei verschiedene Stoffmodelle zur Verfügung. Die dazu erforderlichen Bodenkennwerte können an den Ergebnissen aus Felduntersuchungen, geotechnischen Messungen und Laborversuchen kalibriert werden, z. B. durch die numerische Simulation eines Ödometerversuchs. Um realistische Berechnungsergebnisse zu erhalten, wird die gesamte Belastungsgeschichte des Systems aus Bauwerk und Baugrund abgebildet, also die Abfolge der Bauzustände, die zur Umsetzung der Baumaßnahme geplant sind. Dabei werden auch die veränderlichen hydraulischen Randbedingungen berücksichtigt. Zunehmend wird auch versucht, aus dem Herstellungsvorgang geotechnischer Bauteile (z. B. Pfähle, Schlitzwände) resultierende Effekte bei der Modellbildung zu erfassen.

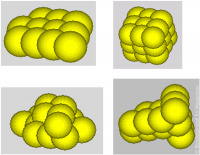
Mit der DEM besteht die Möglichkeit für geometrische Körper wie z. B. Felsblöcke oder Kugeln die Grenzen der FEM bei großen Netzverformungen zu überwinden. Um die Berechnungen zu vereinfachen beschränkt man sich hierbei oft auf Kugelformen und erzeugt mit Kugelhaufen andere Geometrien wie z. B. polygonalgeformte Wasserbausteine.

---

zurück zu: Numerische Verfahren