Analytische Verfahren: Unterschied zwischen den Versionen
Aus BAWiki
Keine Bearbeitungszusammenfassung |
Die LinkTitles-Erweiterung hat automatisch Links zu anderen Seiten hinzugefügt (<a target="_blank" rel="nofollow noreferrer noopener" class="external free" href="https://github.com/bovender/LinkTitles">https://github.com/bovender/LinkTitles</a>). |
||
| Zeile 2: | Zeile 2: | ||
[[Datei:05_Analytische_V_02.jpg|200px|thumb|right|Bild 2: Erddruckbruchmechanismen]] | [[Datei:05_Analytische_V_02.jpg|200px|thumb|right|Bild 2: Erddruckbruchmechanismen]] | ||
[[Datei:05_Analytische_V_03.jpg|200px|thumb|right|Bild 3: Grundbruchschema]]Im Zusammenhang mit der vertikalen Zusammendrückung steht zum Beispiel die Anwendung des Bettungsmodulverfahrens. Hier werden auf Grundlage von berechneten Verformungen Bettungsziffern ermittelt, die wiederum bei der Bemessung von Bauteilen zum Einsatz kommen. Dem Verfahren liegt die vereinfachte Annahme eines Federmodells zugrunde, einer Proportionalität zwischen den Sohlnormalspannungen und der Setzung. Der Bettungsmodul kann mithilfe einer Setzungsberechnung unter Annahme einer vereinfachten linearen Sohldruckverteilung iterativ ermittelt werden. Trotz der Vereinfachungen war das Verfahren für lange Zeit die einzige Methode, um bei der Setzungsermittlung die Interaktion zwischen Bauwerk und Boden rechnerisch abzubilden. Eine weiterführende Methode zur Ermittlung von Verformungen und Spannungen und zur Erfassung der Wechselwirkungen stellen numerische Verfahren dar. Für feinkörnige Böden wie Ton und Schluff können mithilfe von analytischen Verfahren auch zeitlich verzögerte Setzungsvorgänge wie Konsolidierungssetzungen und Kriechen betrachtet werden. | [[Datei:05_Analytische_V_03.jpg|200px|thumb|right|Bild 3: Grundbruchschema]]Im Zusammenhang mit der vertikalen Zusammendrückung steht zum Beispiel die Anwendung des Bettungsmodulverfahrens. Hier werden auf Grundlage von berechneten Verformungen Bettungsziffern ermittelt, die wiederum bei der Bemessung von Bauteilen zum Einsatz kommen. Dem Verfahren liegt die vereinfachte Annahme eines Federmodells zugrunde, einer Proportionalität zwischen den Sohlnormalspannungen und der Setzung. Der Bettungsmodul kann mithilfe einer Setzungsberechnung unter Annahme einer vereinfachten linearen Sohldruckverteilung iterativ ermittelt werden. Trotz der Vereinfachungen war das Verfahren für lange Zeit die einzige Methode, um bei der Setzungsermittlung die Interaktion zwischen Bauwerk und Boden rechnerisch abzubilden. Eine weiterführende Methode zur Ermittlung von Verformungen und Spannungen und zur Erfassung der Wechselwirkungen stellen [[numerische Verfahren]] dar. Für feinkörnige Böden wie Ton und Schluff können mithilfe von analytischen Verfahren auch zeitlich verzögerte Setzungsvorgänge wie Konsolidierungssetzungen und Kriechen betrachtet werden. | ||
[[Datei:05_Analytische_V_04.jpg|200px|thumb|right|Bild 4: Böschungsbruchschema]]Grenzzustände eines Erdkörpers sind zum Beispiel das Erreichen des aktiven oder passiven Erddrucks bei horizontaler Verschiebung einer Wand, der Grundbruch oder das Durchstanzen unter einem Fundament bei zu großer Belastung oder der Böschungsbruch. Klassische Fragestellungen sind dabei die Ermittlung der vorhandenen Sicherheit gegen das Auftreten des Grenzzustandes bzw. das Versagen des entsprechenden Bauteils. Die entsprechenden Berechnungsverfahren sind normativ geregelt. | [[Datei:05_Analytische_V_04.jpg|200px|thumb|right|Bild 4: Böschungsbruchschema]]Grenzzustände eines Erdkörpers sind zum Beispiel das Erreichen des aktiven oder passiven Erddrucks bei horizontaler Verschiebung einer Wand, der Grundbruch oder das Durchstanzen unter einem Fundament bei zu großer Belastung oder der Böschungsbruch. Klassische Fragestellungen sind dabei die Ermittlung der vorhandenen [[Sicherheit]] gegen das Auftreten des Grenzzustandes bzw. das Versagen des entsprechenden Bauteils. Die entsprechenden Berechnungsverfahren sind normativ geregelt. | ||
Grundlage der analytischen Verfahren zur Betrachtung von Grenzzuständen ist die Ermittlung der zutreffenden Traglast. Hierzu bedient man sich der Kollapstheoreme der Plastomechanik. Das statische Kollapstheorem (Unteres-Schranken-Theorem) besagt, dass ein Körper nicht versagt, wenn es (mindestens) ein zulässiges Spannungsfeld gibt, das die statischen Randbedingungen und die Gleichgewichtsbedingungen erfüllt. Das kinematische Kollapstheorem (Oberes-Schranken-Theorem) besagt, dass ein Boden versagt, wenn ein Bruchmechanismus existiert, bei dem die Leistung der äußeren Kräfte die innere Arbeit zur Überwindung der Scherfestigkeit übersteigt. Lösungen nach dem Unteren-Schranken-Theorem grenzen die Traglast von unten ein, liegen also auf der sicheren Seite. In der Praxis kommt wegen der einfacheren Handhabbarkeit in der überwiegenden Zahl der Fälle das kinematische Kollapstheorem zur Anwendung. Hierzu wird eine ausreichende Anzahl von kinematisch möglichen (starr-plastischen) Bruchmechanismen untersucht und so der Bruchmechanismus mit der kleinsten [[Sicherheit|Sicherheit]] gegen Versagen bestimmt. | Grundlage der analytischen Verfahren zur Betrachtung von Grenzzuständen ist die Ermittlung der zutreffenden Traglast. Hierzu bedient man sich der Kollapstheoreme der Plastomechanik. Das statische Kollapstheorem (Unteres-Schranken-Theorem) besagt, dass ein Körper nicht versagt, wenn es (mindestens) ein zulässiges Spannungsfeld gibt, das die statischen Randbedingungen und die Gleichgewichtsbedingungen erfüllt. Das kinematische Kollapstheorem (Oberes-Schranken-Theorem) besagt, dass ein Boden versagt, wenn ein Bruchmechanismus existiert, bei dem die Leistung der äußeren Kräfte die innere Arbeit zur Überwindung der Scherfestigkeit übersteigt. Lösungen nach dem Unteren-Schranken-Theorem grenzen die Traglast von unten ein, liegen also auf der sicheren Seite. In der Praxis kommt wegen der einfacheren Handhabbarkeit in der überwiegenden Zahl der Fälle das kinematische Kollapstheorem zur Anwendung. Hierzu wird eine ausreichende Anzahl von kinematisch möglichen (starr-plastischen) Bruchmechanismen untersucht und so der Bruchmechanismus mit der kleinsten [[Sicherheit|Sicherheit]] gegen Versagen bestimmt. | ||
Aktuelle Version vom 22. Oktober 2022, 00:58 Uhr
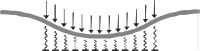
Mithilfe von analytischen Verfahren werden in der klassischen Geotechnik vor allen Dingen die vertikale Zusammendrückung des Baugrundes (Setzungen und Hebungen) betrachtet und das Verhalten von Erdstoffen im Grenzzustand beurteilt.
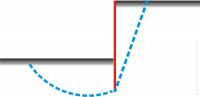

Im Zusammenhang mit der vertikalen Zusammendrückung steht zum Beispiel die Anwendung des Bettungsmodulverfahrens. Hier werden auf Grundlage von berechneten Verformungen Bettungsziffern ermittelt, die wiederum bei der Bemessung von Bauteilen zum Einsatz kommen. Dem Verfahren liegt die vereinfachte Annahme eines Federmodells zugrunde, einer Proportionalität zwischen den Sohlnormalspannungen und der Setzung. Der Bettungsmodul kann mithilfe einer Setzungsberechnung unter Annahme einer vereinfachten linearen Sohldruckverteilung iterativ ermittelt werden. Trotz der Vereinfachungen war das Verfahren für lange Zeit die einzige Methode, um bei der Setzungsermittlung die Interaktion zwischen Bauwerk und Boden rechnerisch abzubilden. Eine weiterführende Methode zur Ermittlung von Verformungen und Spannungen und zur Erfassung der Wechselwirkungen stellen numerische Verfahren dar. Für feinkörnige Böden wie Ton und Schluff können mithilfe von analytischen Verfahren auch zeitlich verzögerte Setzungsvorgänge wie Konsolidierungssetzungen und Kriechen betrachtet werden.
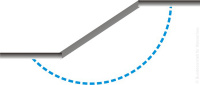
Grenzzustände eines Erdkörpers sind zum Beispiel das Erreichen des aktiven oder passiven Erddrucks bei horizontaler Verschiebung einer Wand, der Grundbruch oder das Durchstanzen unter einem Fundament bei zu großer Belastung oder der Böschungsbruch. Klassische Fragestellungen sind dabei die Ermittlung der vorhandenen Sicherheit gegen das Auftreten des Grenzzustandes bzw. das Versagen des entsprechenden Bauteils. Die entsprechenden Berechnungsverfahren sind normativ geregelt.
Grundlage der analytischen Verfahren zur Betrachtung von Grenzzuständen ist die Ermittlung der zutreffenden Traglast. Hierzu bedient man sich der Kollapstheoreme der Plastomechanik. Das statische Kollapstheorem (Unteres-Schranken-Theorem) besagt, dass ein Körper nicht versagt, wenn es (mindestens) ein zulässiges Spannungsfeld gibt, das die statischen Randbedingungen und die Gleichgewichtsbedingungen erfüllt. Das kinematische Kollapstheorem (Oberes-Schranken-Theorem) besagt, dass ein Boden versagt, wenn ein Bruchmechanismus existiert, bei dem die Leistung der äußeren Kräfte die innere Arbeit zur Überwindung der Scherfestigkeit übersteigt. Lösungen nach dem Unteren-Schranken-Theorem grenzen die Traglast von unten ein, liegen also auf der sicheren Seite. In der Praxis kommt wegen der einfacheren Handhabbarkeit in der überwiegenden Zahl der Fälle das kinematische Kollapstheorem zur Anwendung. Hierzu wird eine ausreichende Anzahl von kinematisch möglichen (starr-plastischen) Bruchmechanismen untersucht und so der Bruchmechanismus mit der kleinsten Sicherheit gegen Versagen bestimmt.
Analytische Verfahren zur Berechnung von Grundwasserströmungen sind auf folgender Seite beschrieben.
Analytische Verfahren - Grundwasserströmung
zurück zu: Geotechnische Methoden
