Nichtlineare, probabilistische Berechnungen: Unterschied zwischen den Versionen
Aus BAWiki
Keine Bearbeitungszusammenfassung |
Die LinkTitles-Erweiterung hat automatisch Links zu anderen Seiten hinzugefügt (<a target="_blank" rel="nofollow noreferrer noopener" class="external free" href="https://github.com/bovender/LinkTitles">https://github.com/bovender/LinkTitles</a>). |
||
| (Eine dazwischenliegende Version von einem anderen Benutzer wird nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
[[Datei:10_Probabilistische_Berech_01.jpg|200px|thumb|right|Bild 1: Rissbildung in einem Nischenausschnitt aus unbewehrtem Beton bei 3D-Verteilung der Druckfestigkeit im Lasteintragungsbereich]]Das BAWMerkblatt TbW* ermöglicht in einem gestuften Verfahren die Anwendung detaillierterer Untersuchungsmethoden, wenn ihre Tragfähigkeit nach aktuellem Regelwerk formal nicht direkt nachweisbar ist. Im Folgenden wird der Einsatz nichtlinearer, probabilistischer Berechnungen am Beispiel von Materialkennwerten vorgestellt: Aus der breiten Streuung der Zusammensetzung und Durchmischung der Baustoffe im Massivbau ergibt sich der Ansatz, einen 5%-Quantil-Wert für Materialkennwerte zu verwenden. | [[Datei:10_Probabilistische_Berech_01.jpg|200px|thumb|right|Bild 1: Rissbildung in einem Nischenausschnitt aus unbewehrtem Beton bei 3D-Verteilung der Druckfestigkeit im Lasteintragungsbereich]]Das BAWMerkblatt TbW* ermöglicht in einem gestuften Verfahren die Anwendung detaillierterer Untersuchungsmethoden, wenn ihre [[Tragfähigkeit]] nach aktuellem Regelwerk formal nicht direkt nachweisbar ist. Im Folgenden wird der Einsatz nichtlinearer, probabilistischer Berechnungen am Beispiel von Materialkennwerten vorgestellt: Aus der breiten Streuung der Zusammensetzung und Durchmischung der Baustoffe im Massivbau ergibt sich der Ansatz, einen 5%-Quantil-Wert für Materialkennwerte zu verwenden. | ||
Die ersten Stufen nach TbW setzen diesen Wert entsprechend des Materials und Bauzeitraums an oder sehen Versuche vor, die wiederum in 5%-Quantil-Werten münden. In der dritten Stufe nach TbW dienen FEM-Simulationen einer möglichst realistischen Abbildung des nichtlinearen Materialverhaltens und der Einsatz probabilistischer Methoden ermöglicht eine Berücksichtigung der erwarteten Bandbreite des verbauten Baustoffs. | Die ersten Stufen nach TbW setzen diesen Wert entsprechend des Materials und Bauzeitraums an oder sehen Versuche vor, die wiederum in 5%-Quantil-Werten münden. In der dritten Stufe nach TbW dienen FEM-Simulationen einer möglichst realistischen Abbildung des nichtlinearen Materialverhaltens und der Einsatz probabilistischer Methoden ermöglicht eine Berücksichtigung der erwarteten Bandbreite des verbauten Baustoffs. | ||
[[Datei:10_Probabilistische_Berech_02.jpg|200px|thumb|right|Bild 2: Rissbildung und Ausbruch in einem Nischenausschnitt aus unbewehrtem Beton mit 3D-Verteilung der Druckfestigkeit im Lasteintragungsbereich]]Hierfür folgen die Materialeigenschaften einer Kennwertsdistribution, welche dem FEM-Modell in einer räumlichen Verteilung aufgeprägt wird. Die 3-D Variation kann je nach Ausprägung maßgebend für die Tragfähigkeit des Bauteils sein und stellt somit selbst einen Designparameter dar. In Szenarien wird die Robustheit verschiedener Kombinationen aus räumlicher Distribution und typischer Variationsbreite der Materialkennwerte untersucht. Aus den jeweiligen Bauteilverhalten ergeben sich die Versagenswahrscheinlichkeiten und das Zuverlässigkeitsniveau für die betrachteten Lastfälle. Beispielhaft zeigen Bild 1 und Bild 2 die unterschiedliche Rissbildung und Schädigung für einen Nischenausschnitt für dieselbe Lasteinbringung und Kennwertsdistribution, aber bei unterschiedlicher räumlicher Verteilung. | [[Datei:10_Probabilistische_Berech_02.jpg|200px|thumb|right|Bild 2: Rissbildung und Ausbruch in einem Nischenausschnitt aus unbewehrtem Beton mit 3D-Verteilung der Druckfestigkeit im Lasteintragungsbereich]]Hierfür folgen die Materialeigenschaften einer Kennwertsdistribution, welche dem FEM-[[Modell]] in einer räumlichen Verteilung aufgeprägt wird. Die 3-D Variation kann je nach Ausprägung maßgebend für die [[Tragfähigkeit]] des Bauteils sein und stellt somit selbst einen Designparameter dar. In Szenarien wird die Robustheit verschiedener Kombinationen aus räumlicher Distribution und typischer Variationsbreite der Materialkennwerte untersucht. Aus den jeweiligen Bauteilverhalten ergeben sich die Versagenswahrscheinlichkeiten und das Zuverlässigkeitsniveau für die betrachteten Lastfälle. Beispielhaft zeigen Bild 1 und Bild 2 die unterschiedliche Rissbildung und Schädigung für einen Nischenausschnitt für dieselbe Lasteinbringung und Kennwertsdistribution, aber bei unterschiedlicher räumlicher Verteilung. | ||
*TbW: Bundesanstalt für Wasserbau (Hg.) (2016): BAWMerkblatt Bewertung der Tragfähigkeit bestehender, massiver Wasserbauwerke (TbW). Karlsruhe: Bundesanstalt für Wasserbau (BAW-Merkblätter, -Empfehlungen und -Richtlinien). | *TbW: [[Bundesanstalt für Wasserbau]] (Hg.) (2016): BAWMerkblatt Bewertung der [[Tragfähigkeit]] bestehender, massiver Wasserbauwerke (TbW). Karlsruhe: [[Bundesanstalt für Wasserbau]] (BAW-Merkblätter, -Empfehlungen und -Richtlinien). | ||
---- | |||
Zurück zu: [[Bautechnische Methoden]] | |||
---- | |||
[[Strukturübersicht]] | |||
[[en:Non-linear probabilistic calculations]] | |||
Aktuelle Version vom 22. Oktober 2022, 01:00 Uhr
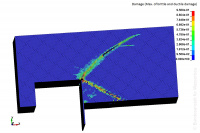
Das BAWMerkblatt TbW* ermöglicht in einem gestuften Verfahren die Anwendung detaillierterer Untersuchungsmethoden, wenn ihre Tragfähigkeit nach aktuellem Regelwerk formal nicht direkt nachweisbar ist. Im Folgenden wird der Einsatz nichtlinearer, probabilistischer Berechnungen am Beispiel von Materialkennwerten vorgestellt: Aus der breiten Streuung der Zusammensetzung und Durchmischung der Baustoffe im Massivbau ergibt sich der Ansatz, einen 5%-Quantil-Wert für Materialkennwerte zu verwenden.
Die ersten Stufen nach TbW setzen diesen Wert entsprechend des Materials und Bauzeitraums an oder sehen Versuche vor, die wiederum in 5%-Quantil-Werten münden. In der dritten Stufe nach TbW dienen FEM-Simulationen einer möglichst realistischen Abbildung des nichtlinearen Materialverhaltens und der Einsatz probabilistischer Methoden ermöglicht eine Berücksichtigung der erwarteten Bandbreite des verbauten Baustoffs.
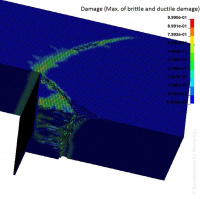
Hierfür folgen die Materialeigenschaften einer Kennwertsdistribution, welche dem FEM-Modell in einer räumlichen Verteilung aufgeprägt wird. Die 3-D Variation kann je nach Ausprägung maßgebend für die Tragfähigkeit des Bauteils sein und stellt somit selbst einen Designparameter dar. In Szenarien wird die Robustheit verschiedener Kombinationen aus räumlicher Distribution und typischer Variationsbreite der Materialkennwerte untersucht. Aus den jeweiligen Bauteilverhalten ergeben sich die Versagenswahrscheinlichkeiten und das Zuverlässigkeitsniveau für die betrachteten Lastfälle. Beispielhaft zeigen Bild 1 und Bild 2 die unterschiedliche Rissbildung und Schädigung für einen Nischenausschnitt für dieselbe Lasteinbringung und Kennwertsdistribution, aber bei unterschiedlicher räumlicher Verteilung.
- TbW: Bundesanstalt für Wasserbau (Hg.) (2016): BAWMerkblatt Bewertung der Tragfähigkeit bestehender, massiver Wasserbauwerke (TbW). Karlsruhe: Bundesanstalt für Wasserbau (BAW-Merkblätter, -Empfehlungen und -Richtlinien).
Zurück zu: Bautechnische Methoden
