Einfluss des Anströmwinkels: Unterschied zwischen den Versionen
Aus BAWiki
imported>Merkel Jennifer Keine Bearbeitungszusammenfassung |
(Die LinkTitles-Erweiterung hat automatisch Links zu anderen Seiten hinzugefügt (<a target="_blank" rel="nofollow noreferrer noopener" class="external free" href="https://github.com/bovender/LinkTitles">https://github.com/bovender/LinkTitles</a>).) |
||
| (2 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 6: | Zeile 6: | ||
''Bild 14: Übersichtsplan der Versuchsrinne mit Messpegeln und eingebauten Streichwehrvarianten'' | ''Bild 14: Übersichtsplan der Versuchsrinne mit Messpegeln und eingebauten Streichwehrvarianten'' | ||
Der Querschnitt des Modells bestand dabei aus einem schmalkronigen Streichwehr mit einer Wanddicke von d = 2,5 cm und einer ausgerundeten Wehrkrone mit r = 1,25 cm. Der Schnittpunkt von Wehrachse und Gerinneachse befand sich dabei ungefähr 12,0 m unterstrom des Einlaufs. Untersucht wurden Streichwehre mit einer Neigung von α = 20°, α = 30°, α = 50°, α = 70° und α = 90° (Bild 14). | Der Querschnitt des Modells bestand dabei aus einem schmalkronigen Streichwehr mit einer Wanddicke von d = 2,5 cm und einer ausgerundeten Wehrkrone mit r = 1,25 cm. Der Schnittpunkt von Wehrachse und Gerinneachse befand sich dabei ungefähr 12,0 m unterstrom des Einlaufs. Untersucht wurden Streichwehre mit einer [[Neigung]] von α = 20°, α = 30°, α = 50°, α = 70° und α = 90° (Bild 14). | ||
{| class="wikitable" | {| class="wikitable" | ||
| Zeile 12: | Zeile 12: | ||
! style="background-color:#FFFFFF;" | [[Bild:schmalkronig.png|thumb|left]] || style="background-color:#FFFFFF;" | [[Bild:Ueberfallbeiwert_schmalkronig.png|350px|thumb|left]] | ! style="background-color:#FFFFFF;" | [[Bild:schmalkronig.png|thumb|left]] || style="background-color:#FFFFFF;" | [[Bild:Ueberfallbeiwert_schmalkronig.png|350px|thumb|left]] | ||
|} | |} | ||
''Bild 15: Schmalkroniges Streichwehr im Labormodell und Definitionsskizze (links) sowie Überfallbeiwert µ bei vollkommenem Überfall in Abhängigkeit vom Anströmwinkel (rechts)'' | ''Bild 15: Schmalkroniges Streichwehr im Labormodell und Definitionsskizze (links) sowie Überfallbeiwert µ bei vollkommenem [[Überfall]] in Abhängigkeit vom Anströmwinkel (rechts)'' | ||
Die Untersuchungsergebnisse für den vollkommenen Überfall zeigen, dass der Überfallbeiwert mit steigender Überfallhöhe h<sub>1</sub> zunimmt, der Einfluss des Anströmwinkels aber so klein ist, dass er bei der hydraulischen Bemessung vernachlässigt und die volle Überfalllänge L angesetzt werden kann (Bild 15). | Die Untersuchungsergebnisse für den vollkommenen [[Überfall]] zeigen, dass der Überfallbeiwert mit steigender [[Überfallhöhe]] h<sub>1</sub> zunimmt, der Einfluss des Anströmwinkels aber so klein ist, dass er bei der hydraulischen Bemessung vernachlässigt und die volle Überfalllänge L angesetzt werden kann (Bild 15). | ||
Steigt der Unterwasserstand an, so kommt es allmählich zu einer Beeinflussung des Oberwasserstandes. Der Abfluss über das Wehr ist rückstaubeeinflusst und man spricht vom unvollkommenen Überfall. Bild 16 zeigt für die untersuchten Anströmgeschwindigkeiten am schmalkronigen Wehr den Einfluss des Rückstaus auf die Überfallhöhe im Modellmaßstab. Die Messwerte können sehr gut mit einer Regressionskurve beschrieben werden und zeigen nur eine geringe Streuung. Die Überfallhöhe h<sub>1</sub> ist weitgehend unabhängig vom Anströmwinkel. | Steigt der Unterwasserstand an, so kommt es allmählich zu einer Beeinflussung des Oberwasserstandes. Der [[Abfluss]] über das [[Wehr]] ist rückstaubeeinflusst und man spricht vom unvollkommenen [[Überfall]]. Bild 16 zeigt für die untersuchten Anströmgeschwindigkeiten am schmalkronigen [[Wehr]] den [[Einfluss des Rückstaus]] auf die [[Überfallhöhe]] im Modellmaßstab. Die Messwerte können sehr gut mit einer Regressionskurve beschrieben werden und zeigen nur eine geringe Streuung. Die [[Überfallhöhe]] h<sub>1</sub> ist weitgehend unabhängig vom Anströmwinkel. | ||
[[Bild:EinflussUnterwasser_schmalkronig.png]] | [[Bild:EinflussUnterwasser_schmalkronig.png]] | ||
''Bild 16: Darstellung der Überfallhöhe h<sub>1</sub> in Abhängigkeit vom spezifischen Abfluss q für das schmalkronige Streichwehr bei unterschiedlichen Anströmwinkeln und Unterwasserständen'' | ''Bild 16: Darstellung der [[Überfallhöhe]] h<sub>1</sub> in Abhängigkeit vom spezifischen [[Abfluss]] q für das schmalkronige Streichwehr bei unterschiedlichen Anströmwinkeln und Unterwasserständen'' | ||
Zur Bestimmung des Rückstaueinflusses führte Schmidt (1957) einen Abminderungskoeffizient σ<sub>uv</sub> ein, welcher in der Poleni-Formel berücksichtigt werden kann (siehe [[Formeln zur Berechnung der hydraulischen Leistungsfähigkeit]]). | Zur Bestimmung des Rückstaueinflusses führte Schmidt (1957) einen Abminderungskoeffizient σ<sub>uv</sub> ein, welcher in der Poleni-Formel berücksichtigt werden kann (siehe [[Formeln zur Berechnung der hydraulischen Leistungsfähigkeit]]). | ||
| Zeile 25: | Zeile 25: | ||
[[Bild: Rückstaueinfluss_schmalkronig.png|thumb|Bild 17: Dimensionslose Darstellung des Rückstaueinflusses für das schmalkronige Streichwehr]] | [[Bild: Rückstaueinfluss_schmalkronig.png|thumb|Bild 17: Dimensionslose Darstellung des Rückstaueinflusses für das schmalkronige Streichwehr]] | ||
Bild 17 zeigt eine dimensionslose Darstellung des Rückstaueinflusses beim schmalkronigen Streichwehr, dem die Abminderungskoeffizienten σ<sub>uv</sub> für das scharfkantige und das breitkronige Wehr gegenübergestellt sind. Dabei ist im Vergleich zum breitkronigen Wehr ein deutlich früher einsetzender Rückstaueinfluss festzustellen, vergleichbar mit dem des senkrecht angeströmten scharfkantigen Wehres. Es zeigt sich weiterhin, dass mit zunehmendem Anströmwinkel tendenziell ein späterer Rückstaueinfluss zu beobachten ist. Obwohl die Streuung in Bild 16 gering ist, ergibt sich bei der Überführung des Rückstaueinflusses in eine dimensionslose Darstellung (Bild 17) ein vergleichsweise großer Streuungsbereich für die untersuchten Anströmwinkel. Abweichungen in der Überfallhöhe von weniger als ±1 mm wirken sich hier relativ stark auf den Abminderungskoeffizient σuv aus. Zu berücksichtigen ist dabei, dass die Berechnung von σ<sub>uv</sub> iterativ erfolgt: Unter Berücksichtigung der Streuung ergibt sich für den Oberwasserstand h<sub>1</sub> bei gegebenem Abfluss Q eine Genauigkeit von ±3 %. Umgekehrt ergibt sich für den Abfluss Q bei gegebener Überfallhöhe h<sub>1</sub> eine Genauigkeit von ±5 %. | Bild 17 zeigt eine dimensionslose Darstellung des Rückstaueinflusses beim schmalkronigen Streichwehr, dem die Abminderungskoeffizienten σ<sub>uv</sub> für das scharfkantige und das breitkronige [[Wehr]] gegenübergestellt sind. Dabei ist im Vergleich zum breitkronigen [[Wehr]] ein deutlich früher einsetzender Rückstaueinfluss festzustellen, vergleichbar mit dem des senkrecht angeströmten scharfkantigen Wehres. Es zeigt sich weiterhin, dass mit zunehmendem Anströmwinkel tendenziell ein späterer Rückstaueinfluss zu beobachten ist. Obwohl die Streuung in Bild 16 gering ist, ergibt sich bei der Überführung des Rückstaueinflusses in eine dimensionslose Darstellung (Bild 17) ein vergleichsweise großer Streuungsbereich für die untersuchten Anströmwinkel. Abweichungen in der [[Überfallhöhe]] von weniger als ±1 mm wirken sich hier relativ stark auf den Abminderungskoeffizient σuv aus. Zu berücksichtigen ist dabei, dass die Berechnung von σ<sub>uv</sub> iterativ erfolgt: Unter Berücksichtigung der Streuung ergibt sich für den Oberwasserstand h<sub>1</sub> bei gegebenem [[Abfluss]] Q eine Genauigkeit von ±3 %. Umgekehrt ergibt sich für den [[Abfluss]] Q bei gegebener [[Überfallhöhe]] h<sub>1</sub> eine Genauigkeit von ±5 %. | ||
==Literatur== | ==Literatur== | ||
Aktuelle Version vom 21. Oktober 2022, 10:17 Uhr
Auf Basis der numerischen Voruntersuchungen wurden im Labor der BAW mit einer einfachen Geometrie Modelluntersuchungen durchgeführt, zunächst mit dem Ziel, den Einfluss des Anströmwinkels auf die hydraulische Leistungsfähigkeit zu ermitteln. Im zweiten Schritt wurde der eingangs beschriebene dachförmige Querschnitt eingebaut, zuerst mit glatter und dann mit rauer Oberfläche. Für die Untersuchungen stand dabei eine Versuchsrinne mit einer Nutzlänge von etwa 20,0 m und einer Breite von 4,0 m zur Verfügung (Bild 14). Das Streichwehr hatte eine Höhe von etwa 0,20 m.
Betrachtet wurden insgesamt 13 Unterwasserstände bis 0,44 m (y2/w = 2,15), die mit acht Durchflüssen zwischen 25 und 350 l/s kombiniert wurden, sodass sich am Ende etwa 100 Zustände pro untersuchter Geometrie ergaben.
Bild 14: Übersichtsplan der Versuchsrinne mit Messpegeln und eingebauten Streichwehrvarianten
Der Querschnitt des Modells bestand dabei aus einem schmalkronigen Streichwehr mit einer Wanddicke von d = 2,5 cm und einer ausgerundeten Wehrkrone mit r = 1,25 cm. Der Schnittpunkt von Wehrachse und Gerinneachse befand sich dabei ungefähr 12,0 m unterstrom des Einlaufs. Untersucht wurden Streichwehre mit einer Neigung von α = 20°, α = 30°, α = 50°, α = 70° und α = 90° (Bild 14).
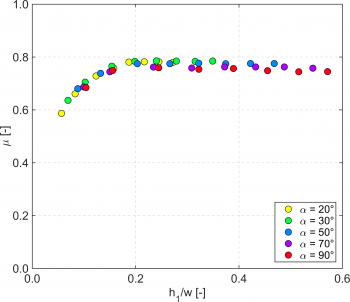
Bild 15: Schmalkroniges Streichwehr im Labormodell und Definitionsskizze (links) sowie Überfallbeiwert µ bei vollkommenem Überfall in Abhängigkeit vom Anströmwinkel (rechts)
Die Untersuchungsergebnisse für den vollkommenen Überfall zeigen, dass der Überfallbeiwert mit steigender Überfallhöhe h1 zunimmt, der Einfluss des Anströmwinkels aber so klein ist, dass er bei der hydraulischen Bemessung vernachlässigt und die volle Überfalllänge L angesetzt werden kann (Bild 15).
Steigt der Unterwasserstand an, so kommt es allmählich zu einer Beeinflussung des Oberwasserstandes. Der Abfluss über das Wehr ist rückstaubeeinflusst und man spricht vom unvollkommenen Überfall. Bild 16 zeigt für die untersuchten Anströmgeschwindigkeiten am schmalkronigen Wehr den Einfluss des Rückstaus auf die Überfallhöhe im Modellmaßstab. Die Messwerte können sehr gut mit einer Regressionskurve beschrieben werden und zeigen nur eine geringe Streuung. Die Überfallhöhe h1 ist weitgehend unabhängig vom Anströmwinkel.
Bild 16: Darstellung der Überfallhöhe h1 in Abhängigkeit vom spezifischen Abfluss q für das schmalkronige Streichwehr bei unterschiedlichen Anströmwinkeln und Unterwasserständen
Zur Bestimmung des Rückstaueinflusses führte Schmidt (1957) einen Abminderungskoeffizient σuv ein, welcher in der Poleni-Formel berücksichtigt werden kann (siehe Formeln zur Berechnung der hydraulischen Leistungsfähigkeit).
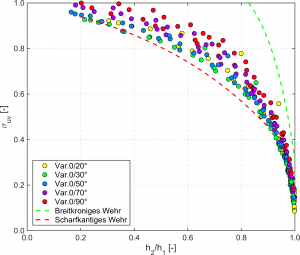
Bild 17 zeigt eine dimensionslose Darstellung des Rückstaueinflusses beim schmalkronigen Streichwehr, dem die Abminderungskoeffizienten σuv für das scharfkantige und das breitkronige Wehr gegenübergestellt sind. Dabei ist im Vergleich zum breitkronigen Wehr ein deutlich früher einsetzender Rückstaueinfluss festzustellen, vergleichbar mit dem des senkrecht angeströmten scharfkantigen Wehres. Es zeigt sich weiterhin, dass mit zunehmendem Anströmwinkel tendenziell ein späterer Rückstaueinfluss zu beobachten ist. Obwohl die Streuung in Bild 16 gering ist, ergibt sich bei der Überführung des Rückstaueinflusses in eine dimensionslose Darstellung (Bild 17) ein vergleichsweise großer Streuungsbereich für die untersuchten Anströmwinkel. Abweichungen in der Überfallhöhe von weniger als ±1 mm wirken sich hier relativ stark auf den Abminderungskoeffizient σuv aus. Zu berücksichtigen ist dabei, dass die Berechnung von σuv iterativ erfolgt: Unter Berücksichtigung der Streuung ergibt sich für den Oberwasserstand h1 bei gegebenem Abfluss Q eine Genauigkeit von ±3 %. Umgekehrt ergibt sich für den Abfluss Q bei gegebener Überfallhöhe h1 eine Genauigkeit von ±5 %.
Literatur
- Schmidt, M. (1957): Gerinnehydraulik, Wiesbaden Bauverlag.
zurück zu Hydraulische Berechnung