Mathematische Verfahren: Unterschied zwischen den Versionen
Aus BAWiki
imported>Mueller-hagedorn Keine Bearbeitungszusammenfassung |
Die LinkTitles-Erweiterung hat automatisch Links zu anderen Seiten hinzugefügt (<a target="_blank" rel="nofollow noreferrer noopener" class="external free" href="https://github.com/bovender/LinkTitles">https://github.com/bovender/LinkTitles</a>). |
||
| (14 dazwischenliegende Versionen von 5 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
[[en:Mathematical Methods]] | [[en:Mathematical Methods]] | ||
[[Bild: Methoden_mathematische_Verfahren.jpg|thumb|Bild 1: Numerik]] | [[Bild: Methoden_mathematische_Verfahren.jpg|thumb|Bild 1: Numerik]] | ||
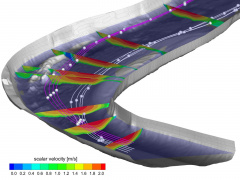
[[Bild: Methoden_mathematische_Verfahren2.jpg|240px|thumb|Bild 2: Dreidimensionale numerische Berechnung der Geschwindigkeitsverteilungen in einer Flusskrümmung.]] | |||
Durch den Einsatz mathematischer Verfahren können Erkenntnisse über natürliche Prozesse gewonnen werden (Simulation). Ferner ermöglichen sie Prognosen zur natürlichen Entwicklung wie auch zur Wirkung anthropogener Eingriffe in natürliche Systeme. Die zentralen [[Simulationsverfahren]] werden von Methoden zur Datenaufbereitung und Gitternetzgenerierung ([[Pre- und Postprocessing|Preprocessing]]) sowie zur Visualisierung und Analyse der Berechnungsergebnisse ([[Pre- und Postprocessing|Postprocessing]]) ergänzt. | Durch den Einsatz mathematischer/numerischer Verfahren können Erkenntnisse über natürliche Prozesse gewonnen werden (Simulation). Ferner ermöglichen sie Prognosen zur natürlichen Entwicklung wie auch zur Wirkung anthropogener Eingriffe in natürliche Systeme. Die zentralen [[Simulationsverfahren]] werden von Methoden zur Datenaufbereitung und Gitternetzgenerierung ([[Pre- und Postprocessing|Preprocessing]]) sowie zur Visualisierung und [[Analyse der Berechnungsergebnisse]] ([[Pre- und Postprocessing|Postprocessing]]) ergänzt. Die numerische Simulation stellt eine etablierte und vielfach eingesetzte Methode zur Bearbeitung verkehrswasserbaulicher Fragestellungen dar. | ||
Bevor ein mathematisches Verfahren eingesetzt werden kann, muss eine Analyse des natürlichen Systems im Hinblick auf die darin ablaufenden Prozesse durchgeführt werden. Mit Blick auf das zu untersuchende System, z.B. Fluss oder Ästuar, sowie auf die zu untersuchende Fragestellung, muss eine Auswahl hinsichtlich der unbedingt von dem Modell zu berücksichtigenden Prozesse durchgeführt werden (Modellfunktionalität). Davon ausgehend wird das konzeptionelle Modell formuliert, zumeist in Form gewöhnlicher oder partieller Differentialgleichungen. Diese können für natürliche Systeme in der Regel nicht exakt gelöst werden. Einzelne Prozesse, wie z.B. die Reibung an der Gewässersohle, können daher nur in vereinfachter Form berücksichtigt werden (Parametrisierung). Darüber hinaus werden die unbekannten Größen (Wasserspiegellage, Strömungsgeschwindigkeit usw.) nur an endlich vielen Orten und Terminen berechnet (Diskretisierung). Aus den grundlegenden Gleichungen sowie den Annahmen zur Diskretisierung und Parametrisierung folgt die algorithmische Implementierung des Modells unter Zuhilfenahme von Methoden der numerischen Mathematik. Dem schließt sich noch die Software-Implementierung an, die an Hand grundlegender Beispiele auf ihre Korrektheit verifiziert wird. Damit steht ein mathematisches Verfahren mit eingeschränktem Gültigkeitsbereich zur Verfügung, welches zur Simulation verschiedener ortsspezifischer Modelle (Rhein bei Bingen, Tideelbe, usw.) eingesetzt werden kann. Für ein breites Spektrum an natürlichen Prozessen können in der Bundesanstalt für Wasserbau (BAW) verschiedene mathematische Verfahren eingesetzt werden. | Bevor ein mathematisches Verfahren eingesetzt werden kann, muss eine Analyse des natürlichen Systems im Hinblick auf die darin ablaufenden Prozesse durchgeführt werden. Mit Blick auf das zu untersuchende System, z.B. Fluss oder [[Ästuar]], sowie auf die zu untersuchende Fragestellung, muss eine Auswahl hinsichtlich der unbedingt von dem [[Modell]] zu berücksichtigenden Prozesse durchgeführt werden (Modellfunktionalität). Davon ausgehend wird das konzeptionelle [[Modell]] formuliert, zumeist in Form gewöhnlicher oder partieller Differentialgleichungen. Diese können für natürliche Systeme in der Regel nicht exakt gelöst werden. Einzelne Prozesse, wie z.B. die Reibung an der [[Gewässersohle]], können daher nur in vereinfachter Form berücksichtigt werden (Parametrisierung). Darüber hinaus werden die unbekannten Größen (Wasserspiegellage, Strömungsgeschwindigkeit usw.) nur an endlich vielen Orten und Terminen berechnet (Diskretisierung). Aus den grundlegenden Gleichungen sowie den Annahmen zur Diskretisierung und Parametrisierung folgt die algorithmische Implementierung des Modells unter Zuhilfenahme von Methoden der numerischen Mathematik. Dem schließt sich noch die Software-Implementierung an, die an Hand grundlegender Beispiele auf ihre Korrektheit verifiziert wird. Damit steht ein mathematisches Verfahren mit eingeschränktem Gültigkeitsbereich zur Verfügung, welches zur Simulation verschiedener ortsspezifischer Modelle (Rhein bei Bingen, [[Tideelbe]], usw.) eingesetzt werden kann. Für ein breites Spektrum an natürlichen Prozessen können in der [[Bundesanstalt für Wasserbau]] (BAW) verschiedene mathematische Verfahren eingesetzt werden. | ||
Im Preprocessing müssen Anfangs- und Randwerte für den gesamten Simulationszeitraum sowie das Berechnungsgitter für das jeweilige ortsspezifische Modell erstellt werden. Die konsistenten Berechnungsergebnisse einer Simulation werden später mit Beobachtungsdaten verglichen (Kalibrierung, Validierung), grafisch visualisiert, zur Verdeutlichung dynamischer Vorgänge zu Animationen verarbeitet, oder zum Berechnen von Kenngrößen (z.B. Hochwasser, maximale Strömungsgeschwindigkeit) sowie deren Änderung (Prognose) weiter gehend analysiert. | Im Preprocessing müssen Anfangs- und Randwerte für den gesamten Simulationszeitraum sowie das Berechnungsgitter für das jeweilige ortsspezifische [[Modell]] erstellt werden. Die konsistenten Berechnungsergebnisse einer Simulation werden später mit Beobachtungsdaten verglichen ([[Kalibrierung]], Validierung), grafisch visualisiert, zur Verdeutlichung dynamischer Vorgänge zu Animationen verarbeitet, oder zum Berechnen von Kenngrößen (z.B. [[Hochwasser]], maximale Strömungsgeschwindigkeit) sowie deren Änderung ([[Prognose]]) weiter gehend analysiert. | ||
==Dokumentationen== | ==Dokumentationen== | ||
* [[BAW-Software-Dokumentation]] | * [[BAW-Software-Dokumentation]] | ||
* [[Pre- und Postprocessing]] | |||
* [[Simulationsverfahren]] | |||
==Validierungsstudien und Modellsysteme== | |||
* [[Validierungsstudien]] | |||
* [[Modellsysteme]] | |||
---- | ---- | ||
Aktuelle Version vom 21. Oktober 2022, 08:53 Uhr

Durch den Einsatz mathematischer/numerischer Verfahren können Erkenntnisse über natürliche Prozesse gewonnen werden (Simulation). Ferner ermöglichen sie Prognosen zur natürlichen Entwicklung wie auch zur Wirkung anthropogener Eingriffe in natürliche Systeme. Die zentralen Simulationsverfahren werden von Methoden zur Datenaufbereitung und Gitternetzgenerierung (Preprocessing) sowie zur Visualisierung und Analyse der Berechnungsergebnisse (Postprocessing) ergänzt. Die numerische Simulation stellt eine etablierte und vielfach eingesetzte Methode zur Bearbeitung verkehrswasserbaulicher Fragestellungen dar.
Bevor ein mathematisches Verfahren eingesetzt werden kann, muss eine Analyse des natürlichen Systems im Hinblick auf die darin ablaufenden Prozesse durchgeführt werden. Mit Blick auf das zu untersuchende System, z.B. Fluss oder Ästuar, sowie auf die zu untersuchende Fragestellung, muss eine Auswahl hinsichtlich der unbedingt von dem Modell zu berücksichtigenden Prozesse durchgeführt werden (Modellfunktionalität). Davon ausgehend wird das konzeptionelle Modell formuliert, zumeist in Form gewöhnlicher oder partieller Differentialgleichungen. Diese können für natürliche Systeme in der Regel nicht exakt gelöst werden. Einzelne Prozesse, wie z.B. die Reibung an der Gewässersohle, können daher nur in vereinfachter Form berücksichtigt werden (Parametrisierung). Darüber hinaus werden die unbekannten Größen (Wasserspiegellage, Strömungsgeschwindigkeit usw.) nur an endlich vielen Orten und Terminen berechnet (Diskretisierung). Aus den grundlegenden Gleichungen sowie den Annahmen zur Diskretisierung und Parametrisierung folgt die algorithmische Implementierung des Modells unter Zuhilfenahme von Methoden der numerischen Mathematik. Dem schließt sich noch die Software-Implementierung an, die an Hand grundlegender Beispiele auf ihre Korrektheit verifiziert wird. Damit steht ein mathematisches Verfahren mit eingeschränktem Gültigkeitsbereich zur Verfügung, welches zur Simulation verschiedener ortsspezifischer Modelle (Rhein bei Bingen, Tideelbe, usw.) eingesetzt werden kann. Für ein breites Spektrum an natürlichen Prozessen können in der Bundesanstalt für Wasserbau (BAW) verschiedene mathematische Verfahren eingesetzt werden.
Im Preprocessing müssen Anfangs- und Randwerte für den gesamten Simulationszeitraum sowie das Berechnungsgitter für das jeweilige ortsspezifische Modell erstellt werden. Die konsistenten Berechnungsergebnisse einer Simulation werden später mit Beobachtungsdaten verglichen (Kalibrierung, Validierung), grafisch visualisiert, zur Verdeutlichung dynamischer Vorgänge zu Animationen verarbeitet, oder zum Berechnen von Kenngrößen (z.B. Hochwasser, maximale Strömungsgeschwindigkeit) sowie deren Änderung (Prognose) weiter gehend analysiert.
Dokumentationen
Validierungsstudien und Modellsysteme
zurück zu: Wasserbauliche Methoden
